
 :
: 和定点
和定点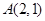 ,由⊙
,由⊙ 外一点
外一点 向⊙
向⊙ 引切线
引切线 ,切点为
,切点为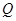 ,且满足
,且满足 .
. 间满足的等量关系;
间满足的等量关系; 长的最小值;
长的最小值; 为圆心所作的⊙
为圆心所作的⊙ 与⊙
与⊙ 有公共点,试求半径取最小值时的⊙
有公共点,试求半径取最小值时的⊙ 方程.
方程. ;(2)
;(2)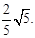 ;(3)
;(3)
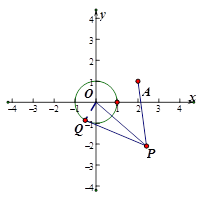
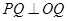 ,在
,在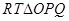 中,
中,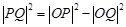 ,且
,且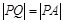 ,结合两点之间距离公式可得关于
,结合两点之间距离公式可得关于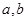 的等式;(2)在
的等式;(2)在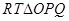 中,
中,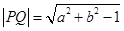 ,是含有
,是含有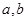 的二元函数,结合(1)可得关于
的二元函数,结合(1)可得关于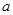 的一元函数,求其最小值即可;(3)方法一:因为⊙
的一元函数,求其最小值即可;(3)方法一:因为⊙ 与⊙
与⊙ 有公共点,则得圆心距和其半径的关系
有公共点,则得圆心距和其半径的关系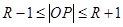 即
即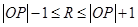 ,要求半径
,要求半径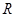 的最小值,只需
的最小值,只需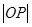 最小,将
最小,将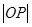 用两点之间距离公式表示出来,求其最小值并求取的最小值时
用两点之间距离公式表示出来,求其最小值并求取的最小值时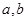 ,得⊙
,得⊙ 的圆心,进而求出圆的标准方程;方法二:由(1)知⊙
的圆心,进而求出圆的标准方程;方法二:由(1)知⊙ 的圆心的轨迹方程为
的圆心的轨迹方程为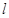 :
: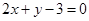 ,过点
,过点 作垂直于
作垂直于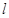 的垂线,垂足为
的垂线,垂足为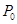 ,当两圆外切且以
,当两圆外切且以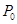 为圆心时,半径最小,此时
为圆心时,半径最小,此时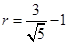 ,两条直线求交点确定圆心,从而求出圆的 标准方程.
,两条直线求交点确定圆心,从而求出圆的 标准方程.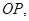
 为切点,
为切点,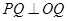 ,由勾股定理有
,由勾股定理有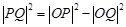 ,又由已知
,又由已知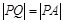 ,故
,故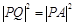 .即:
.即: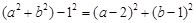 ,化简得实数a、b间满足的等量关系为:
,化简得实数a、b间满足的等量关系为: ;(2)由
;(2)由 ,得
,得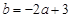 ,
,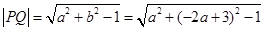
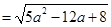 =
=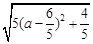 ,故当
,故当 时,
时, 即线段PQ长的最小值为
即线段PQ长的最小值为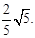 ;
;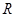 ,
, 圆P与圆O有公共点,圆O的半径为1,
圆P与圆O有公共点,圆O的半径为1,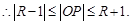 即
即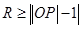 且
且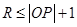 ,而
,而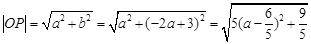 ,故当
,故当 时,
时,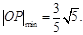 此时,
此时, 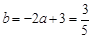 ,
,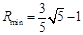 ,得半径取最小值时圆P的方程为
,得半径取最小值时圆P的方程为 .
. 与圆
与圆 有公共点,圆
有公共点,圆 半径最小时为与圆外
半径最小时为与圆外 切(取小者)的情形,而这些半径的最小值为圆心
切(取小者)的情形,而这些半径的最小值为圆心 到直线
到直线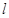 的距离减去1,圆心为
的距离减去1,圆心为 过原点与
过原点与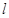 垂直的直线
垂直的直线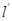 与
与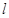 的交点
的交点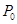 ,
,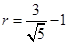 ,又
,又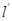 :x-2y = 0,解方程组
:x-2y = 0,解方程组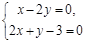 ,得
,得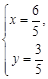 .即
.即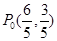 ,∴所求圆方程为
,∴所求圆方程为 .
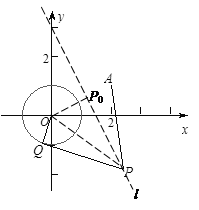
.


科目:高中数学 来源:不详 题型:填空题
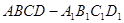 ,下列说法正确的有: ____________.
,下列说法正确的有: ____________.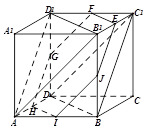
 点在线段
点在线段 上运动,棱锥
上运动,棱锥 体积不变;
体积不变;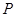 点在线段
点在线段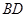 上运动,直线AP与平面
上运动,直线AP与平面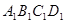 平行;
平行;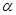 截此正方体,如果截面是三角形,则必为锐角三角形;
截此正方体,如果截面是三角形,则必为锐角三角形;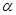 截此正方体,如果截面是四边形,则必为平行四边形;
截此正方体,如果截面是四边形,则必为平行四边形;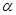 截正方体得到一个六边形(如图所示),则截面
截正方体得到一个六边形(如图所示),则截面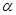 在平面
在平面 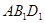 与平面
与平面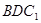 间平行移动时此六边形周长先增大,后减小。
间平行移动时此六边形周长先增大,后减小。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,棱长为1,黑白二蚁都从点
,棱长为1,黑白二蚁都从点 出发,沿棱向前爬行,每走一条棱称为“走完一段”.白蚁爬行的路线是
出发,沿棱向前爬行,每走一条棱称为“走完一段”.白蚁爬行的路线是 黑蚁爬行的路线是
黑蚁爬行的路线是 它们都遵循如下规则:所爬行的第
它们都遵循如下规则:所爬行的第 段所在直线与第
段所在直线与第 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中 ).设黑白二蚁走完第2014段后,各停止在正方体的某个顶点处,这时黑白蚁的距离是 ( )
).设黑白二蚁走完第2014段后,各停止在正方体的某个顶点处,这时黑白蚁的距离是 ( )
| A.1 | B. | C. | D. 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com