已知f(x)＝ex－ax－1.
(1)求f(x)的单调增区间；
(2)若f(x)在定义域R内单调递增，求a的取值范围．
（1）当a≤0时，f(x)的单调增区间为(－∞，＋∞)；当a>0时，f(x)的单调增区间为(ln a，＋∞)．（2）(－∞，0]．
【解析】(1)∵f(x)＝ex－ax－1(x∈R)，∴f′(x)＝ex－a.令f′(x)≥0，得ex≥a.当a≤0时，f′(x)>0在R上恒成立；当a>0时，有x≥ln a．综上，当a≤0时，f(x)的单调增区间为(－∞，＋∞)；当a>0时，f(x)的单调增区间为(ln a，＋∞)．
(2)由(1)知f′(x)＝ex－a.∵f(x)在R上单调递增，
∴f′(x)＝ex－a≥0恒成立，即a≤ex在R上恒成立．
∵x∈R时，ex>0，∴a≤0，
即a的取值范围是(－∞，0]．
阅读快车系列答案科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练优化重组卷2练习卷（解析版） 题型：解答题
在△ABC中，角A，B，C对应的边分别是a，b，c.已知cos 2A－3cos(B＋C)＝1.
(1)求角A的大小；
(2)若△ABC的面积S＝5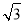
，b＝5，求sin Bsin C的值．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练x4-1练习卷（解析版） 题型：填空题
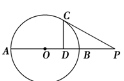
如图，点P在圆O直径AB的延长线上，且PB＝OB＝2，PC切圆O于C点，CD⊥AB于D点，则CD＝________.
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练5练习卷（解析版） 题型：解答题
已知x＝3是函数f(x)＝aln(1＋x)＋x2－10x的一个极值点．
(1)求a；
(2)求函数f(x)的单调区间；
(3)若直线y＝b与函数y＝f(x)的图象有3个交点，求b的取值范围．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练5练习卷（解析版） 题型：选择题
函数f(x)的定义域是R，f(0)＝2，对任意x∈R，f(x)＋f′(x)>1，则不等式ex·f(x)>ex＋1的解集为( )．
A. 
B.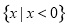 
C. 
D.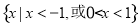 
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练4练习卷（解析版） 题型：选择题
已知函数f(x)＝x3＋ax2＋x＋2(a>0)的极大值点和极小值点都在区间(－1,1)内，则实数a的取值范围是( )．
A．(0,2] B．(0,2) C．[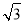
，2) D．(
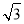，2)
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练3练习卷（解析版） 题型：填空题
(2013·广东卷)给定区域D：
令点集T＝{(x0，y0)∈D|x0，y0∈Z，(x0，y0)是z＝x＋y在D上取得最大值或最小值的点}，则T中的点共确定________条不同的直线．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习专题提升训练2练习卷（解析版） 题型：选择题
已知函数f(x)＝
则函数f(x)的零点为 ( )．
A.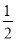 
，0 B．－2,0 C．
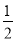D．0
查看答案和解析>>
科目：高中数学 来源：2014年高考数学（理）二轮复习6-1直线与圆练习卷（解析版） 题型：选择题
当直线l：y＝k(x－1)＋2被圆C：(x－2)2＋(y－1)2＝5截得的弦最短时，k的值为( )．
A．2 B.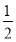 
C．3 D．1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com