
已知函数 ,其中
,其中 ,
, 是自然对数的底数.
是自然对数的底数.
(1)求函数 的零点;
的零点;
(2)若对任意 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知 ,且函数
,且函数 在R上是单调函数,探究函数
在R上是单调函数,探究函数 的单调性.
的单调性.
(1)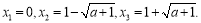 (2)
(2)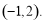 (3)函数
(3)函数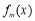 在R上是减函数
在R上是减函数
【解析】
试题分析:(1)
把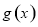 的零点问题转化为方程
的零点问题转化为方程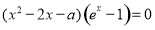 的根的问题.
的根的问题.
(2)因为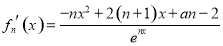 ,由题设可知
,由题设可知 有两个两点,其中一个在
有两个两点,其中一个在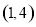 ,一个在
,一个在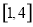 外
外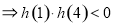 ,解这个不等式,可得实数
,解这个不等式,可得实数 的取值范围.
的取值范围.
(3)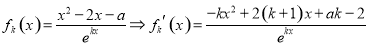
由函数 在R上是单调函数,所以
在R上是单调函数,所以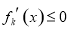 ,得到
,得到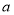 与
与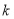 的关系,然后由此关系推出
的关系,然后由此关系推出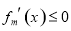 .
.
试题解析:
【解析】
(1) ,
,
令g(x)=0, 有ex-1=0,即x=0;或 x2-2x-a=0;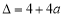 ,
,
①当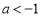 时,
时,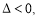 函数
函数 有1个零点
有1个零点 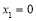 ; 1分
; 1分
②当 时,
时,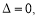 函数
函数 有2个零点
有2个零点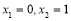 ;2分
;2分
③当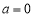 时,
时,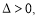 函数
函数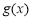 有两个零点
有两个零点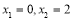 ;3分
;3分
④当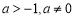 时,
时,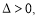 函数
函数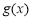 有三个零点:
有三个零点:
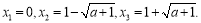 4分
4分
(2)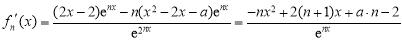 ,5分
,5分
设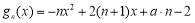 ,
,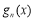 的图像是开口向下的抛物线,
的图像是开口向下的抛物线,
由题意对任意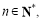
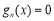 有两个不等实数根
有两个不等实数根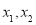 ,
,
且 则对任意
则对任意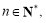
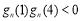 ,
,
即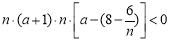 ,有
,有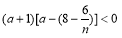 ,7分
,7分
又任意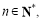
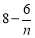 关于
关于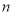 递增,
递增, 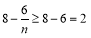 ,
,
故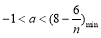 ,所以
,所以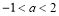 .
.
所以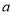 的取值范围是
的取值范围是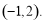 9分
9分
(3)由(2)知, 存在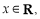
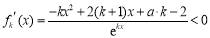 ,又函数
,又函数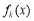 在R上是单调函数,故函数
在R上是单调函数,故函数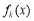 在R上是单调减函数, 10分
在R上是单调减函数, 10分
对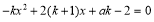 来说
来说
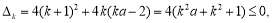 即
即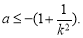 11分
11分
所以对于函数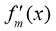 来说
来说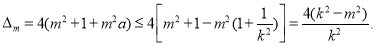
由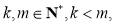 知
知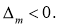 12分
12分
即对任意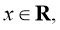
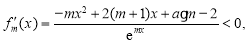
故函数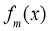 在R上是减函数. 13分
在R上是减函数. 13分
考点:1、函数的零点;2、利用导数研究函数的单调性;3、一元二次方程根的分布.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试理科数学试卷(解析版) 题型:选择题
函数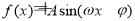 (
(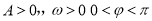 )的图象如图所示,则
)的图象如图所示,则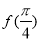 的值为( )
的值为( )
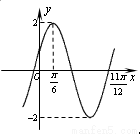
A.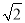 B.
B.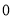 C.
C.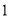 D.
D.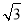
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考理科数学试卷(解析版) 题型:选择题
已知 ,把数列
,把数列 的各项排列成如下的三角形状,
的各项排列成如下的三角形状,
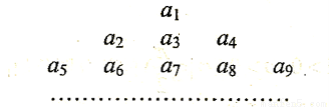
记 表示第
表示第 行的第
行的第 个数,则
个数,则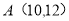 = ( )
= ( )
A. B.
B. C.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考文科数学试卷(解析版) 题型:选择题
“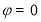 ”是“函数
”是“函数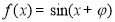 为奇函数”的( )
为奇函数”的( )
A.充分非必要条件 B. 必要非充分条件
C.充要条件 D. 非充分非必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试理科数学试卷(解析版) 题型:填空题
函数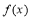 的定义域为A,若
的定义域为A,若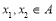 且
且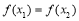 时总有
时总有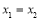 ,则称
,则称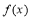 为单函数.例如,函数
为单函数.例如,函数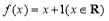 是单函数.下列命题:
是单函数.下列命题:
①函数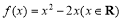 是单函数;
是单函数;
②函数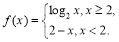 是单函数;
是单函数;
③若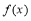 为单函数,
为单函数, 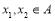 且
且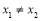 ,则
,则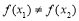 ;
;
④若函数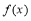 在定义域内某个区间D上具有单调性,则
在定义域内某个区间D上具有单调性,则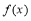 一定是单函数.
一定是单函数.
其中真命题是 (写出所有真命题的编号).
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试理科数学试卷(解析版) 题型:选择题
以下四个命题中:
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②两个随机变量的线性相关性越强,相关系数的绝对值越接近于1;
③在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为0.8 ;
④对分类变量X与Y的随机变量k2的观测值k来说,k越小,判断“X与Y有关系”的把握程度越大.
其中真命题的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试文科数学试卷(解析版) 题型:填空题
设关于x,y的不等式组 表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是
表示的平面区域内存在点P(x0,y0)满足x0-2y0=2,则m的取值范围是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com