
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学 | 120 | 105 | 91 | 124 | 85 | 132 | 121 | 100 | 78 | 135 |
| 化学 | 70 | 68 | 74 | 82 | 78 | 71 | 81 | 62 | 54 | 90 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 132 | 92 | 85 | 123 | 100 | 97 | 101 | 96 | 103 | 105 |
| 化学 | 85 | 65 | 53 | 77 | 63 | 85 | 73 | 45 | 84 | 72 |
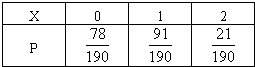
| ||
|
| 78 |
| 190 |
| ||||
|
| 91 |
| 190 |
| ||
|
| 21 |
| 190 |
| 78 |
| 190 |
| 91 |
| 190 |
| 21 |
| 190 |
| 7 |
| 10 |
| 数学优秀 | 数学不优秀 | 合计 | |
| 化学优秀 | 4 | 2 | 6 |
| 化学不优秀 | 3 | 11 | 14 |
| 合计 | 7 | 13 | 20 |
| 20×(4×11-3×2)2 |
| 6×7×13×14 |


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
| 年份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 | 八月 | 九月 | 十月 |
| 2010 | 1.5 | 2.7 | 2.4 | 2.8 | 3.1 | 2.9 | 3.3 | 3.5 | 3.6 | 4.4 |
| 2011 | 4.9 | 4.9 | 5.4 | x | y | 6.4 | 6.5 | 6.2 | 6.1 | 5.5 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
| x1+x2+Lxn |
| n |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省吉安市高二(下)期末数学试卷(理科)(解析版) 题型:解答题
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学 | 120 | 105 | 91 | 124 | 85 | 132 | 121 | 100 | 78 | 135 |
| 化学 | 70 | 68 | 74 | 82 | 78 | 71 | 81 | 62 | 54 | 90 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 132 | 92 | 85 | 123 | 100 | 97 | 101 | 96 | 103 | 105 |
| 化学 | 85 | 65 | 53 | 77 | 63 | 85 | 73 | 45 | 84 | 72 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省遂宁市射洪中学高二(上)期中数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com