
分析 由三角函数的周期性和对称性,以及诱导公式可得.
解答 解:由题意可得函数的周期为T$\frac{2π}{\frac{π}{5}}$=10,
由三角函数的对称性计算可得f(1)+f(2)+f(3)+…+f(10)=0,
∴f(1)+f(2)+f(3)+…+f(2014)=f(1)+f(2)+f(3)+f(4)
=cos$\frac{π}{5}$+cos$\frac{2π}{5}$+cos$\frac{3π}{5}$+cos$\frac{4π}{5}$=cos$\frac{π}{5}$+cos$\frac{2π}{5}$+cos(π-$\frac{2π}{5}$)+cos($π-\frac{π}{5}$)
=cos$\frac{π}{5}$+cos$\frac{2π}{5}$-cos$\frac{2π}{5}$-cos$\frac{π}{5}$=0
点评 本题考查余弦函数的图象和周期性,属基础题.


科目:高中数学 来源: 题型:解答题
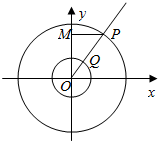 如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.
如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学/分 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 |
| 物理/分 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学/分 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
| 物理/分 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
| 数学成绩优秀 | 数学成绩不优秀 | 合计 | |
| 物理成绩优秀 | 5 | 2 | 17 |
| 物理成绩不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
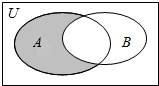 设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )
设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则图中阴影部分表示的集合为( )| A. | {1,2,5,6} | B. | {1} | C. | {2} | D. | {1,2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com