
过点P(1,4)引一条直线,使它在两条坐标轴上的截距为正值,且它们的和最小,求这条直线的方程.
解:(解法1)设所求的直线方程为y-4=k(x-1).显见,上述直线在x轴、y轴上的截距分别为1-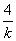 、4-k.由于1-
、4-k.由于1-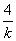 >0且4-k>0可得,k<0.直线在两坐标轴上的截距之和为S=
>0且4-k>0可得,k<0.直线在两坐标轴上的截距之和为S=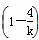 +(4-k)=5+(-k)+
+(4-k)=5+(-k)+ ≥5+4=9,当且仅当-k=-
≥5+4=9,当且仅当-k=-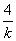 ,即k=-2时,S有最小值9.故所求直线方程为y-4=-2(x-1),即2x+y-6=0.
,即k=-2时,S有最小值9.故所求直线方程为y-4=-2(x-1),即2x+y-6=0.
(解法2)设所求的直线方程为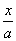 +
+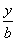 =1(a>0,b>0).
=1(a>0,b>0).
据题设有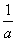 +
+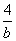 =1,① 令S=a+b.②
=1,① 令S=a+b.②
①×②,有S=(a+b)  =5+
=5+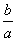 +
+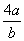 ≥5+4=9.当且仅当
≥5+4=9.当且仅当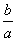 =
=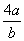 时,即2a=b,且
时,即2a=b,且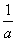 +
+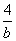 =1,也即a=3,b=6时,取等号.
=1,也即a=3,b=6时,取等号.
故所求的直线方程为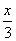 +
+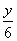 =1,即2x+y-6=0.
=1,即2x+y-6=0.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
已知函数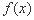 的定义域为
的定义域为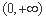 ,若
,若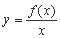 在
在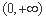 上为增函数,则称
上为增函数,则称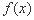 为“一阶比增函数”.
为“一阶比增函数”.
(1)若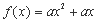 是“一阶比增函数”,求实数
是“一阶比增函数”,求实数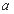 的取值范围;
的取值范围;
(2)若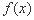 是“一阶比增函数”,当
是“一阶比增函数”,当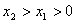 时,试比较
时,试比较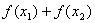 与
与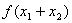 的大小;
的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:
设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1) 若l在两坐标轴上截距相等,求l的方程;
(2) 若l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com