Question

实数x、y满足=1，试求x-y的最大值与最小值，并指出何时取得最大值与最小值.

Answer 1

思路分析：本题的思考方式也许容易想到由已知方程予以变形代换，但容易看到会出现开方，很不利于求x-y的最大值与最小值.这时，根据已知条件可考虑借助于相应的参数方程来求解，借助于正弦、余弦的有界性从而把问题解决.

解：由已知可设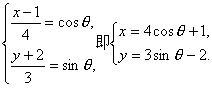

则x-y=(4cosθ+1)-(3sinθ-2)=(4cosθ-3sinθ)+3=5cos(θ+α)+3，

其中cosα=,sinα=.当cos(θ+α)=1,即θ+α=2kπ,k∈Z时，

cosθ=cos(2kπ-α)=cosα=，sinθ=sin(2kπ-α)=-sinα=.

∴x=4×+1=,y=3×()-2=时，x-y的最大值为8.

同理,当x=,y=时，x-y的最小值为-2.

    误区警示 本题易错点主要有两点:(1)对于椭圆的参数方程不会转化而直接使用普通方程；(2)在使用参数方程运算时不考虑α的实际取值.