
(本小题满分14分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
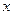 | 3 | 4 | 5 | 6 |
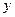 | 2.5 | 3 | 4 | 4.5 |
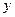 关于
关于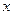 的线性回归方程
的线性回归方程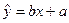 ;
; 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下: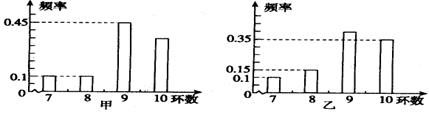
若将频率视为概率,回答下列问题:
(I)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(II)若甲、乙两运动员各自射击1次,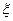 表示这2次射击中击中9环以上(含9环)的次数,求
表示这2次射击中击中9环以上(含9环)的次数,求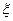 的分布列及
的分布列及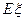 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某公司近年来科研费用支出 万元与公司所获得利润
万元与公司所获得利润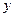 万元之间有如下的统计数据:
万元之间有如下的统计数据:
 | 2 | 3 | 4 | 5 |
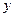 | 18 | 27 | 32 | 35 |
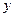 关于
关于 的线性回归方程
的线性回归方程 ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下: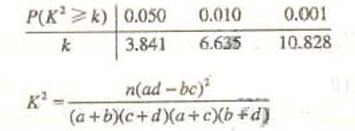
| 是否需要志愿 性别 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)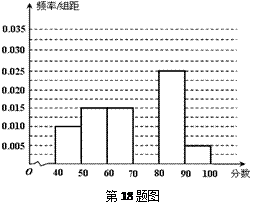
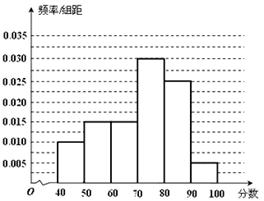
某校从参加高一年级期中考试的学生中随机抽取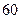 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
,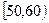 …
…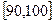 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为 的学生中抽取一个容量为
的学生中抽取一个容量为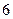 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取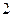 人,求至多有
人,求至多有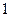 人在分数段
人在分数段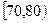 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
随机抽取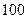 名学生,测得他们的身高(单位:
名学生,测得他们的身高(单位: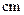 ),按照区间
),按照区间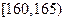 ,
,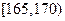 ,
,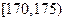 ,
,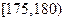 ,
,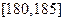 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).
(Ⅰ)求频率分布直方图中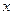 的值及身高在
的值及身高在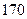
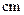 以上的学生人数;
以上的学生人数;
(Ⅱ)将身高在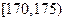 ,
,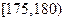 ,
,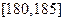 区间内的学生依次记为
区间内的学生依次记为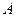 ,
,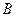 ,
,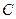 三个组,用分层抽样的方法从三个组中抽取
三个组,用分层抽样的方法从三个组中抽取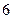 人,求从这三个组分别抽取的学生人数;
人,求从这三个组分别抽取的学生人数;
(Ⅲ)在(Ⅱ)的条件下,要从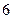 名学生中抽取
名学生中抽取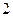 人,用列举法计算
人,用列举法计算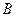 组中至少有
组中至少有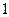 人被抽中的概率.
人被抽中的概率.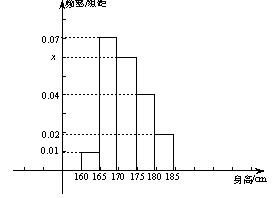
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为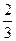 和
和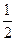 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数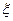 的分布列与期望.w.w.w.k.s.5.u.c.o.m
的分布列与期望.w.w.w.k.s.5.u.c.o.m 

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com