
(本小题满分14分)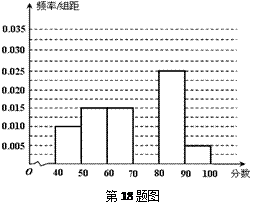
某校从参加高一年级期中考试的学生中随机抽取 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
,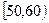 …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(3)用分层抽样的方法在分数段为 的学生中抽取一个容量为
的学生中抽取一个容量为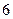 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取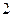 人,求至多有
人,求至多有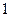 人在分数段
人在分数段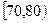 的概率.
的概率.
71,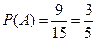
解析
解析:(Ⅰ)分数在 内的频率为:
内的频率为: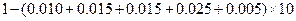
 ,故
,故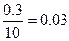 ,
,
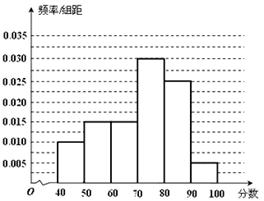
如图所示: -----------------------4分
(求频率2分,作图2分)
(Ⅱ)平均分为: .------------7分
.------------7分
(Ⅲ)由题意,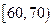 分数段的人数为:
分数段的人数为: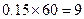 人; ks5u
人; ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
----------------8分 分数段的人数为:
分数段的人数为: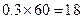 人; ks5u
人; ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
----------------9分
∵在 的学生中抽取一个容量为
的学生中抽取一个容量为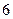 的样本,
的样本,
∴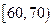 分数段抽取2人,分别记为
分数段抽取2人,分别记为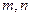 ;
; 分数段抽取4人,分别记为
分数段抽取4人,分别记为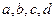 ;
;
设从样本中任取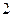 人,至多有1人在分数段
人,至多有1人在分数段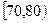 为事件
为事件 ,则基本事件空间包含的基本事件有:
,则基本事件空间包含的基本事件有: 、
、 、
、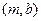 、
、 、
、 、……、
、……、 共15种,
共15种,
则事件 包含的基本事件有:
包含的基本事件有: 、
、 、
、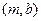 、
、 、
、 、
、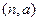 、
、 、
、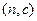 、
、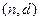 共9种,--- ks5u
共9种,--- ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u
ks5u


科目:高中数学 来源: 题型:解答题
(本题满分13分)某种产品的广告费支出 (单位:百万元)与销售额
(单位:百万元)与销售额 (单位:百万元)之间有如下对应数据
(单位:百万元)之间有如下对应数据
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
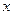 | 3 | 4 | 5 | 6 |
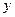 | 2.5 | 3 | 4 | 4.5 |
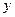 关于
关于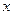 的线性回归方程
的线性回归方程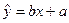 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校为了调查喜欢语文学科与性别是否有关系,随机调查了50名学生,男生中有12人不喜欢语文,有10人喜欢语文,女生中有8人不喜欢语文,有20人喜欢语文,根据所给数据,
(1)写出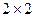 列联表;
列联表;
(2)由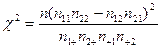 ,及临界值3.841和6.635作统计分析推断。
,及临界值3.841和6.635作统计分析推断。
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
学校周三要排语文、数学、英语、物理、化学和生物6门不同的课程,若第一节不排语文且第六节排生物,则不同的排法共有( )
| A.96种 | B.120种 | C.216种 | D.240种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
为了检测某种产品的直径(单位mm),抽取了一个容量为100的样本,其频率分布表(不完整)如下:
| 分组 | 频数累计 | 频数 | 频率 |
| [10.75,10.85) | 6 | 6 | 0.06 |
| [10.85,10.95) | 15 | 9 | 0.09 |
| [10.95,11.05) | 30 | 15 | 0.15 |
| [11.05,11.15) | 48 | 18 | 0.18 |
| [11.15,11.25) | ▲ | ▲ | ▲ |
| [11.25,11.35) | 84 | 12 | 0.12 |
| [11.35,11.45) | 92 | 8 | 0.08 |
| [11.45,11.55) | 98 | 6 | 0.06 |
| [11.55,11.65) | 100 | 2 | 0.02 |
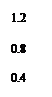
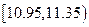 范围内的可能性是百分之几?
范围内的可能性是百分之几?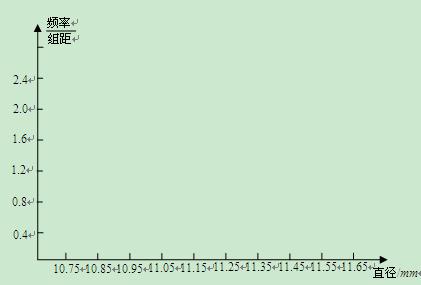
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)为考察某种药物预防疾病的效果,进行动物试验,调查k!s#5^uk!s#5^u了105个样本,统计结果为:服药的共有55个样本,服药但患病的仍有10个样本,没有服药且未患病的有30个样本.
(1)根据所给样本数据完成2×2列联表中的数据;
(2)请问能有多大把握认为药物有效?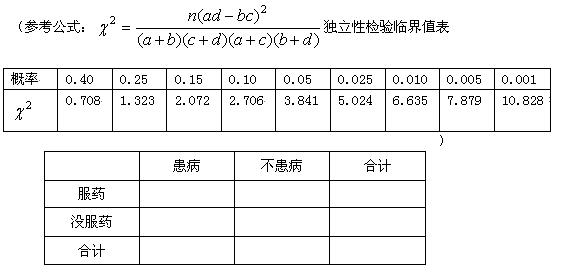
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:
(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(Ⅲ)根据(Ⅱ)的结论,能否提出更好的调查办法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由。
附: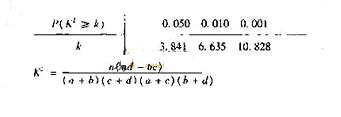
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com