Question

若点P、Q分别在函数y＝e^x和函数 y＝lnx的图象上，则P、Q两点间的距离的最小值是     ．

 

Answer 1

【答案】

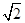
【解析】

试题分析：考虑到两曲线关于直线y=x对称，求丨PQ丨的最小值可转化为求P到直线y=x的最小距离，再利用导数的几何意义，求曲线上斜率为1的切线方程，从而得此距离。解：∵曲线y=e^x与曲线y=lnx互为反函数，其图象关于y=x对称，故可先求点P到直线y=x的最近距离d，设曲线y=e^x上斜率为1的切线为y=x+b，∵y’=e^x，由e^x=1，得x=0，故切点坐标为（0，1），即b=1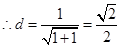 ，∴丨PQ丨的最小值为2d=2

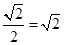
考点：互为反函数的函数图象的对称性

点评：本题主要考查了互为反函数的函数图象的对称性，以及导数的几何意义，曲线的切线方程的求法，同时考查了化归的思想方法，属于中档题