
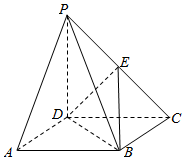
 如图,在四棱锥P-ABCD中,底图ABCD是正方形,PD⊥平面ABCD,E是PC的中点
如图,在四棱锥P-ABCD中,底图ABCD是正方形,PD⊥平面ABCD,E是PC的中点分析 (1)根据线面平行的判定定理证明OE∥PA即可证明PA∥平面BDE,
(2)根据三棱锥的体积公式,利用转化法,进行求解即可.
解答 证明:(1)连接AC,设AC,BD的交点为O,连OE,
由O,E分别为AC,CP中点,
∴OE∥PA
又OE?平面EDB,PA?平面EDB,
∴PA∥平面EDB.
(2)∵PD⊥平面ABCD,CD?平面平面ABCD,
∴PD⊥DC,
∵E是PC的中点,且PD=DC=2,
∴S△PDE=$\frac{1}{2}$S△PDC=$\frac{1}{2}×\frac{1}{2}×{2}^{2}=1$,
∵PD⊥平面ABCD,AD?平面平面ABCD,
∴PD⊥AD,
∵AD⊥CD,PD∩CD=D,
∴AD⊥平面PDC,
∵BC∥AD.
∴BC⊥平面PDC,
则VP-EDB=VB-PDE=$\frac{1}{3}$S△PDE|BC|=$\frac{1}{3}×1×2$=$\frac{2}{3}$.
点评 本题主要考查线面平行的判定以及三棱锥体积的计算,根据转化法转化为比较好计算的三棱锥的体积是解决本题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
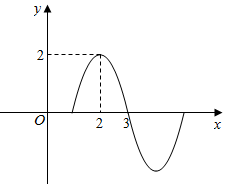 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(2016)=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(2016)=( )| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -$\frac{10}{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1,4) | B. | (-2,1,-4) | C. | (2,1,-4) | D. | (2,-1,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overline{y}$=1.5$\overline{x}$-15 | B. | 15是回归系数a | ||
| C. | 1.5是回归系数a | D. | 当x=10时,y的准确值为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6和2.4 | B. | 6和5.6 | C. | 2和5.6 | D. | 2和2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{69}{56}$ | B. | $\frac{7}{8}$ | C. | $\frac{69}{28}$ | D. | $\frac{7}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com