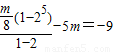已知数列an,点P(an,an+1)(n∈N*)在一次函数y=2x+m的图象上,数列bn满足条件bn=an+1-an(n∈N*,b1≠0).
(I)求证:数列bn是等比数列;
(II)设数列an,bn的前n项和分别为Sn、Tn且S6=T4,S5=-9,求实数m的值.
【答案】
分析:(Ⅰ)由题设知a
n+1=2a
n+m,所以a
n+1+m=2(a
n+m),又b
n=a
n+1-a
n=2(a
n+m)-a
n=a
n+m,b
n+1=a
n+1+m=2(a
n+m)=2b
n,且b
1=a
1+m≠0,由此证明数列b
n是以a
1+m为首项,公比为2的等比数列.
(Ⅱ)由S
6=T
4b
n=a
n+m,知a
1+a
2+…+a
5+a
6=a
1+a
2+a
3+a
4+4m,a
5+a
6=4m.由(Ⅰ)知b
n=(a
1+m)×2
n-1,则a
n=(a
1+m)•2
n-1-m,由此可求出实数m的值.
解答:解:(Ⅰ)∵P(a
n,a
n+1)在一次函数y=2x+m的图象上∴a
n+1=2a
n+m
∴a
n+1+m=2(a
n+m)又b
n=a
n+1-a
n=2(a
n+m)-a
n=a
n+m
∴b
n+1=a
n+1+m=2(a
n+m)=2b
n,且b
1=a
1+m≠0
∴数列b
n是以a
1+m为首项,公比为2的等比数列(6分)
(Ⅱ)∵S
6=T
4b
n=a
n+m
∴a
1+a
2+…+a
5+a
6=a
1+a
2+a
3+a
4+4m
∴a
5+a
6=4m(7分)
由(Ⅰ)知b
n=(a
1+m)×2
n-1即a
n+m=(a
1+m)•2
n-1则a
n=(a
1+m)•2
n-1-m
∴(a
1+m)×2
4-m+(a
1+m)×2
5-m=4m
∴
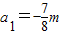
(10分)
∵S
5=-9a
n+m是以2为公比的等比数列∴
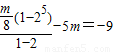
解得:m=8(12分)
点评:本题考查数列的性质和综合应用,解题时要注意公式的合理运用.

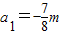 (10分)
(10分)