
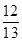 ,cos C=
,cos C=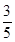 .
.
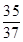 min(3)
min(3)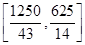
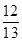 ,cos C=
,cos C=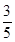 ,所以sin A=
,所以sin A=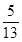 ,
,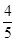 .
.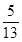 ×
×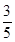 +
+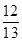 ×
×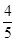 =
=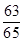 .
.
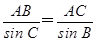 ,得AB=
,得AB=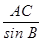 ×sin C=
×sin C=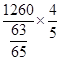 =1040(m).
=1040(m).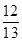 =200(37t2-70t+50),因0≤t≤
=200(37t2-70t+50),因0≤t≤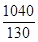 ,即0≤t≤8,故当t=
,即0≤t≤8,故当t=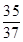 (min)时,甲、乙两游客距离最短.
(min)时,甲、乙两游客距离最短.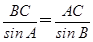 ,得BC=
,得BC=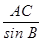 ×sin A=
×sin A=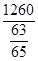 ×
×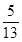 =500(m).
=500(m).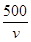 -
-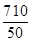 ≤3,解得
≤3,解得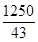 ≤v≤
≤v≤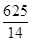 ,所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在
,所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在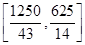 (单位:m/min)范围内
(单位:m/min)范围内

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com