
分析 (1)由正弦定理、诱导公式、两角和的正弦公式化简已知的式子,求出tanB的值,由内角的范围和特殊角的三角函数值求出B;
(2)由AD=AC得∠ACD=∠ADC,设∠DAC=∠BAD=α,∠ACD=∠ADC=β,由内角和定理列出方程组求出α、β,由正弦定理求出AB、AD、AC,由余弦定理列出式子化简后求出CD的值.
解答 解:(1)由bsinA+bcosA=c以及正弦定理得,
sinBsinA+sinBcosA=sinC=sin(A+B),
化简得,sinBsinA-sinAcosB=0,
又sinA≠0,则sinB=cosB,即tanB=1,
因为0<B<180°,所以B=45°;
(2)由AD=AC得,∠ACD=∠ADC,
设∠DAC=∠BAD=α,∠ACD=∠ADC=β,
则$\left\{\begin{array}{l}{45°+2α+β=180°}\\{α+2β=180°}\end{array}\right.$,解得$\left\{\begin{array}{l}{α=30°}\\{β=75°}\end{array}\right.$,
在△ABD中,∠BAD=30°,∠ADB=105°
由正弦定理得,$\frac{AB}{sin∠ADB}=\frac{AD}{sin∠ABD}=\frac{BD}{sin∠BAD}$,
则$\frac{AB}{sin105°}=\frac{AD}{sin45°}=\frac{2}{sin30°}=4$,
所以AB=$\sqrt{6}+\sqrt{2}$,AD=$2\sqrt{2}$,则AC=$2\sqrt{2}$,
由余弦定理得,CD2=AD2+AC2-2•AD•AC•cos∠DAC
=8+8-2×$2\sqrt{2}$×$2\sqrt{2}$×$\frac{\sqrt{3}}{2}$=$4(\sqrt{3}-1)^{2}$,
所以CD=$2(\sqrt{3}-1)$.
点评 本题考查正弦定理、余弦定理,内角和定理,以及诱导公式、两角和的正弦公式等等的应用,考查方程思想,化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\frac{1}{2}$$\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{3}{2}\overrightarrow b+\frac{1}{2}$$\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
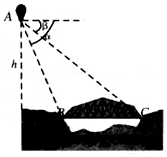 如图,从气球A上测得正前方的河流的两岸B、C的俯角分别为α=60°,β=45°,如果此时气球的高度h是10米,则河流的宽度BC=10-$\frac{10\sqrt{3}}{3}$米.
如图,从气球A上测得正前方的河流的两岸B、C的俯角分别为α=60°,β=45°,如果此时气球的高度h是10米,则河流的宽度BC=10-$\frac{10\sqrt{3}}{3}$米.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “$sinθ=\frac{1}{2}$”是“θ=30°”的充分不必要条件 | |
| B. | 命题p:?n0∈N,${2^{n_0}}>1000$,则¬p:?n∈N,2n≤1000 | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| D. | 命题“若?x∈(0,+∞),则2x<3x”是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正八面体P-ABCD-Q由两个棱长都为a的正四棱锥拼接而成.
如图,正八面体P-ABCD-Q由两个棱长都为a的正四棱锥拼接而成.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com