练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知⊙M：x2+(y-2)2=1,Q是x轴上的动点，QA、QB分别切⊙M于A、B两点.

    （1）若|AB|=，求直线MQ的方程；

    （2）求证：直线AB恒过定点，并求出此定点坐标.

    (1)解析：设AB交MQ于E点，(如下图)则易知MQ垂直平分线段AB，

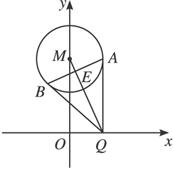
    ∴|ME|=.

    由射影定理知，|MA|2=|ME|·|MQ|，

    ∴|MQ|=.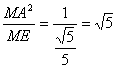

    M（0，2），设Q（a,0）,

    则|MQ|=.

    解得a=±1,即Q（1，0）或Q（-1，0）.

    ∴直线MQ的方程为2x+y-2=0或2x-y+2=0.

    (2)证明：QA、QB是⊙M的切线，则MA⊥AQ，MB⊥BQ，故A、M、B、Q四点共圆且MQ是此圆直径，设此圆圆心为F.设Q（a,0）,则F（,1）,|MQ|=,∴⊙F的方程为即（x-）2+(y-1)2=即x2+y2-ax-2y=0联立x2+(y-2)2=1，消去x2+y2项，即得两圆公共弦AB所在直线的方程：-ax+2y-3=0.

    故直线AB恒过定点（0，）.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

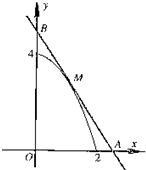    精英家教网如图，已知M是函数y=4-x2（1＜x＜2）的图象C上一点，过M点作曲线C的切线与x轴、y轴分别交于点A，B，O是坐标原点，求△AOB面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知M={(x，y)|y=
    		9-x2
    ，y≠0}    ，N={（x，y）|y=x+b}，若M∩N≠∅，则b∈（　　）
    A、[-3
    		2
    ，3
    		2
    ]
    B、(-3
    		2
    ，3
    		2
    )
    C、(-3，3
    		2
    ]
    D、[-3，3
    		2
    ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•湘潭模拟）已知M={(x，y)|0≤y≤
    		4-x2
    }    ，直线l：y=kx+2k与曲线C：y=
    		4-x2
    有两个不同的交点，设直线l与曲线C围成的封闭区域为P，在区域M内随机取一点A，点A落在区域P内的概率为p，若p∈[
    π-2
    2π
    ，1]    ，则实数k的取值范围为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知⊙M：x2+（y-2）2=1，Q是x轴上的动点，QA、QB分别切⊙M于A、B两点．
    （Ⅰ）求证直线AB恒过一个定点；
    （Ⅱ）求动弦AB的中点P的轨迹方程．

    查看答案和解析>>

    同步练习册答案