
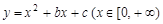 是单调函数的充要条件是
是单调函数的充要条件是A.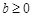 | B.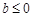 | C.b>0 | D.b<0 |
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,D是BC中点,为确保灌溉的效果,铺设时要求∠EDF=
,D是BC中点,为确保灌溉的效果,铺设时要求∠EDF= 60°。现有两种方案可供参考。甲方案:取AC的中点E铺设水管;乙方案:取AB的中点F铺设水管。
60°。现有两种方案可供参考。甲方案:取AC的中点E铺设水管;乙方案:取AB的中点F铺设水管。
 。试证明该结论的正确性。
。试证明该结论的正确性。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
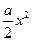 +
+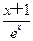 -1.
-1.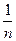 <
<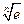 <1+
<1+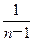 成立.
成立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
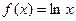 .
.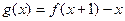 的最大值;
的最大值;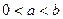 时,求证
时,求证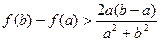 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com