
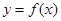 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当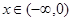 时,
时,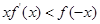 成立,若
成立,若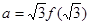 ,
,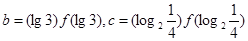 ,则
,则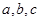 大小关系 ( )
大小关系 ( )A.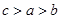 | B.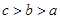 | C.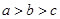 | D.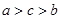 |
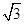 ∈(1,2),∴F(2)>F(
∈(1,2),∴F(2)>F(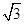 )>F(lg3),∵
)>F(lg3),∵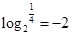 ,从而F(
,从而F(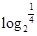 )=F(-2)=F(2),∴F(
)=F(-2)=F(2),∴F(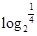 )>F(
)>F(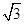 )>F(lg3),即(
)>F(lg3),即(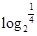 )f(
)f(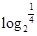 )>
)>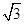 f(
f(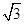 )>(lg3)f(lg3),得c>a>b,故答案为:A
)>(lg3)f(lg3),得c>a>b,故答案为:A

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:不详 题型:填空题
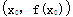 为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题: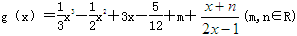 ,
,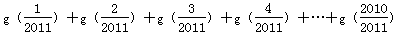 = .
= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com