
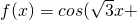 φ)(0<φ<π),且f(x)+f′(x)为奇函数.
φ)(0<φ<π),且f(x)+f′(x)为奇函数.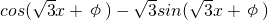 =
=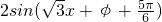 ,
, .
.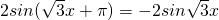 .
.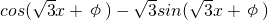 =
=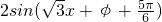 ,
,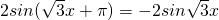 .
.

 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
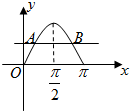 设函数y=sinx(0≤x≤π)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间
设函数y=sinx(0≤x≤π)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
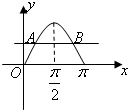 设函数y=sinx(0≤x≤π)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)在[0,
设函数y=sinx(0≤x≤π)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)在[0,| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2013届山东省冠县一中高二下期中学分认定理科数学试卷(解析版) 题型:选择题
设函数 在区间(0,4)上是减函数,则
在区间(0,4)上是减函数,则 的取值范围是 ( )
的取值范围是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com