
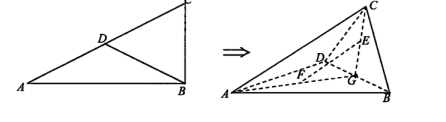
 ,求三棱锥A一BCD的体积.
,求三棱锥A一BCD的体积. .
. 中,利用余弦定理可以求出AG的边长,在
中,利用余弦定理可以求出AG的边长,在 中,利用三个边长的关系,可判断出
中,利用三个边长的关系,可判断出 ,所以利用线面垂直的判定可以得到
,所以利用线面垂直的判定可以得到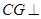 平面ABD,所以CG是锥体的高,利用等体积法将
平面ABD,所以CG是锥体的高,利用等体积法将 转化为
转化为 ,从而求出锥体的体积.
,从而求出锥体的体积. 的中位线
的中位线 EF//AC 3分
EF//AC 3分 平面ABC EF
平面ABC EF 平面ABC
平面ABC EF//平面ABC 6分
EF//平面ABC 6分 中,
中, ,由余弦定理得:
,由余弦定理得: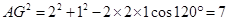 , 8分
, 8分


 AG,又CG
AG,又CG BD
BD 

 平面ABD 10分
平面ABD 10分
 12分
12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com