
����Ŀ��һƬɭ��ԭ���Ϊ![]() ���ƻ���ij�꿪ʼ��ÿ�꿳��һЩ���֣���ÿ�꿳������İٷֱ���ȣ����ƻ�������ԭ�����һ��ʱ������ʱ����10�꣮Ϊ������̬������ɭ���������Ҫ����ԭ�����
���ƻ���ij�꿪ʼ��ÿ�꿳��һЩ���֣���ÿ�꿳������İٷֱ���ȣ����ƻ�������ԭ�����һ��ʱ������ʱ����10�꣮Ϊ������̬������ɭ���������Ҫ����ԭ�����![]() ����֪������Ϊֹ��ɭ��ʣ�����Ϊԭ�����
����֪������Ϊֹ��ɭ��ʣ�����Ϊԭ�����![]() ��
��
��1����ÿ�꿳������İٷֱȣ�
��2��������Ϊֹ����ɭ���ѿ����˶����ꣿ
��3��Ϊ������̬������������ܿ��������ꣿ
���𰸡���1��![]() ����2��������Ϊֹ���ѿ�����5�ꣻ��3��������ܿ���15�꣮
����2��������Ϊֹ���ѿ�����5�ꣻ��3��������ܿ���15�꣮
�������������������1������ÿ�꿳������İٷֱ���ȣ��������������һ��ʱ������ʱ����10�꣬��ÿ�꿳������İٷֱ�Ϊx �ɽ������̣���֮���ɵõ�ÿ�꿳������İٷֱȣ�
��2���辭��m��ʣ�����Ϊԭ����![]() ���������⣺������Ϊֹ��ɭ��ʣ�����Ϊԭ����
���������⣺������Ϊֹ��ɭ��ʣ�����Ϊԭ����![]() �����г�����m�ĵ�ʽ����֮���ɣ�
�����г�����m�ĵ�ʽ����֮���ɣ�
��3������������ӽ��꿪ʼ���Ժ���n�꣬���������n���ʣ������������⣬��������n�IJ��ȹ�ϵ������һЩ���ȹ�ϵ������ý�����ܿ��������꣮
�⣺��1����ÿ�꿳������İٷֱ�Ϊx �� 0��x��1������![]() ��
��
��![]() �����
�����![]()
��2���辭��m��ʣ�����Ϊԭ����![]() ����
����![]() ��
��
��![]() ��
��![]() �����m=5
�����m=5
�ʵ�����Ϊֹ���ѿ�����5�꣮
��3����ӽ��꿪ʼ���Ժ���n�꣬��n���ʣ�����Ϊ![]()
��![]() ��
��![]() ������1��x��n��
������1��x��n��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���n��15
�ʽ�����ܿ���15�꣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ,
,![]() ,����
,����![]() (e����Ȼ����),
(e����Ȼ����),![]()
��1����![]() ʱ, ��
ʱ, ��![]() �ĵ������䡢��ֵ��
�ĵ������䡢��ֵ��
��2���Ƿ����![]() ��ʹ
��ʹ![]() ����Сֵ��3�����������
����Сֵ��3�����������![]() ��ֵ���������ڣ�˵������.
��ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ����������ժ���㷨������ԣ�һ�����й������÷������⣺��1,2,3,4,5,6,7,8,9�ֱ�����![]() �ķ����У�ʹ��ÿһ�У�ÿһ�м��Խ����ϵ��������ĺͶ���ȣ����ǹ涨��ֻҪ�����÷��Ķ�Ӧλ�ã���ÿ�е�һ�еķ����е����ֲ�ȫ��ͬ���ͳ�Ϊ��ͬ�Ļ÷�����ô���в�ͬ�����÷��ĸ����ǣ� ��
�ķ����У�ʹ��ÿһ�У�ÿһ�м��Խ����ϵ��������ĺͶ���ȣ����ǹ涨��ֻҪ�����÷��Ķ�Ӧλ�ã���ÿ�е�һ�еķ����е����ֲ�ȫ��ͬ���ͳ�Ϊ��ͬ�Ļ÷�����ô���в�ͬ�����÷��ĸ����ǣ� ��
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ʒ��Ҫ�����������飬���鷽���ǣ��ȴ�������Ʒ����ȡ4�������飬��4����Ʒ������Ʒ�ļ�����Ϊn.���n��3���ٴ�������Ʒ����ȡ4�������飬����Ϊ����Ʒ����������Ʒͨ�����飻���n��4���ٴ�������Ʒ����ȡ1�������飬��Ϊ����Ʒ����������Ʒͨ�����飻��������£�������Ʒ������ͨ�����飮
����������Ʒ������Ʒ��Ϊ50%����ȡ���IJ�Ʒ������Ʒ�ĸ��ʶ�Ϊ![]() ���Ҹ�����Ʒ�Ƿ�Ϊ����Ʒ�������
���Ҹ�����Ʒ�Ƿ�Ϊ����Ʒ�������
(1)��������Ʒͨ������ĸ��ʣ�
(2)��֪ÿ����Ʒ�������Ϊ100Ԫ������ȡ��ÿ����Ʒ����Ҫ���飬��������Ʒ��������������ķ��ü�ΪX(��λ��Ԫ)����X�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У�������Ϊ����������һ����������洹ֱ��������֮Ϊ���������ĸ��涼Ϊֱ�������ε��������֮Ϊ��Ğ��
��ͼ��������![]() �У�����
������![]() ����
����![]() ����
����![]() ��
�� ![]() Ϊ
Ϊ![]() �е㣬��
�е㣬��![]() ��
��![]() �ϣ���
�ϣ���![]() ƽ��
ƽ��![]() ������
������![]() ��
�� ![]() ��
��
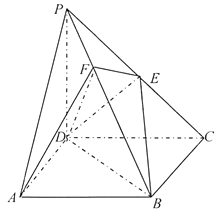
����֤���� ![]() ƽ��
ƽ��![]() ��
��
�������ж�������![]() �Ƿ�Ϊ��Ğ�����ǣ�д����ÿ�����ֱ�ǣ�ֻ��д�����ۣ��������ǣ�˵�����ɣ�
�Ƿ�Ϊ��Ğ�����ǣ�д����ÿ�����ֱ�ǣ�ֻ��д�����ۣ��������ǣ�˵�����ɣ�
������֪![]() ��
�� ![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ2��2������ÿһ������������һ�����֣����ֿ�����1��2��3��4�е��κ�һ���������ظ���������A��������ִ���B��������֣���ͬ�������(����)
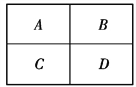
A. 192�� B. 128�� C. 96�� D. 12��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����
����![]() ��
��
��1������![]() ��
��![]() �ϵĵ������䣬������֤����
�ϵĵ������䣬������֤����
��2�������![]() �ķ���
�ķ���![]() ������Ϊ
������Ϊ![]() �������Ƿ����ʵ��
�������Ƿ����ʵ��![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() �������
�������![]() ��
��![]() ������������ڣ����
������������ڣ����![]() ��ȡֵ��Χ���������ڣ�˵�����ɣ�
��ȡֵ��Χ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���ͬѧ�μ�ѧУ��һվ���ס����ػ����������δ��ع����У������سɹ���������⣻��ûͨ������̭����ÿ����ള3�أ��۴���һ�ص�10�֣����ڶ��ص�20�֣��������ص�30�֣�һ�ض�û����û�е÷֣���֪��ÿ�δ��سɹ��ĸ���Ϊ![]() ����ÿ�δ��سɹ��ĸ���Ϊ
����ÿ�δ��سɹ��ĸ���Ϊ![]() ����
����
�������ҵĵ÷�����Ϊ![]() ����
����![]() �÷ֲ��к���ѧ������
�÷ֲ��к���ѧ������
�������ǡ�ñ��Ҷ�30�ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����϶���������������ܶ�ѧУ����Ԫ���ż�ʱ�䣬��ǰ�ż���ѧ�����ڼ��������֣���и��ݡ�֣�������������칫�����ڽ�����Ⱦ������ɫԤ������Ϊ��ɫԤ����֪ͨ��.��12��29��12ʱ����ɫԤ������Ϊ��ɫԤ����12��30��0ʱ����I����Ӧ����ȷҪ��������Сѧ�Ƚ�������ͣ�Σ�ͣ�β�ͣѧ����ѧ���ͼҳ���ͣ����һ�ٴ���һ����Ϊ�˽����ɵģ����µ���ѧϰ���ɵ�.ij�������Ϊ���˽�ڶԸþٴ��̬�ȣ��������ɷ���50�ˣ�����������������ܳ��±���
���䣨�꣩ |
|
|
|
|
|
|
Ƶ�� | 5 | 10 | 15 | 10 | 5 | 5 |
������ | 4 | 6 | 9 | 6 | 3 | 4 |
��1���벹ȫ��������Ա�����Ƶ�ʷֲ�ֱ��ͼ��
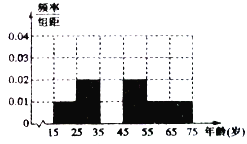
��2������������![]() �ı��������зֱ����ѡȡһ�˽����ٵ��飬�������˶��ɡ�ͣ�Ρ���һ�ٴ�ĸ���.
�ı��������зֱ����ѡȡһ�˽����ٵ��飬�������˶��ɡ�ͣ�Ρ���һ�ٴ�ĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com