
【题目】已知函数![]() ,且
,且![]() .
.
(1)求函数![]() 在
在![]() 上的单调区间,并给以证明;
上的单调区间,并给以证明;
(2)设关于![]() 的方程
的方程![]() 的两根为
的两根为![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得不等式
,使得不等式![]() 对任意的
对任意的![]() 及
及![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)单调递增区间为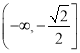 ,单调递减区间为
,单调递减区间为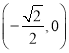 ;
;
(2)存在实数![]() 符合题意,其取值范围是
符合题意,其取值范围是![]() .
.
【解析】试题分析:(1)由![]() 可得
可得![]() ,所以
,所以![]() ,然后利用函数单调性的定义求出函数
,然后利用函数单调性的定义求出函数![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为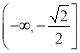 ,单调递减区间为
,单调递减区间为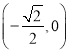 。(2)由题意先求出
。(2)由题意先求出![]() 的最大值为3,所以由题意可得当
的最大值为3,所以由题意可得当![]() ,不等式
,不等式![]() 恒成立,构造函数
恒成立,构造函数![]() ,只需满足
,只需满足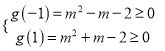 ,解得
,解得![]() 或
或![]() ,由此可得所求范围,从而说明存在实数
,由此可得所求范围,从而说明存在实数![]() 满足题意。
满足题意。
试题解析:
(1)∵![]() ,
,
∴![]() ,
,
∴![]() 。
。
设![]() ,且
,且![]() ,
,
则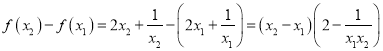 ,
,
①当![]() 时,
时, ![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴函数![]() 在
在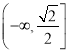 上单调递增;
上单调递增;
②当![]() 时,
时, ![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴函数![]() 在
在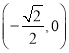 上单调递减,
上单调递减,
∴函数![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为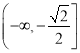 ,单调递减区间为
,单调递减区间为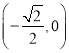 ;
;
(2)由![]() ,得
,得![]() ,
,
∴![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
故由题意得当![]() ,不等式
,不等式![]() 恒成立,
恒成立,
设![]() ,
,
则只须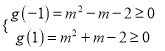 ,
,
解得![]() 或
或![]() ,
,
故存在实数![]() 符合题意,其取值范围是
符合题意,其取值范围是![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,底面ABCD中,AB⊥AD,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
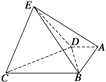
(1)求证:平面DEC⊥平面BDE;
(2)求点A到平面BDE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙二人同时从![]() 地赶住
地赶住![]() 地,甲先骑自行车到两地的中点再改为跑步;乙先跑步到两地的中点再改为骑自行车,最后两人同时到达
地,甲先骑自行车到两地的中点再改为跑步;乙先跑步到两地的中点再改为骑自行车,最后两人同时到达![]() 地.已知甲骑自行车比乙骑自行车的速度快,且两人骑车的速度均大于跑步的速度.现将两人离开
地.已知甲骑自行车比乙骑自行车的速度快,且两人骑车的速度均大于跑步的速度.现将两人离开![]() 地的距离
地的距离![]() 与所用时间
与所用时间![]() 的函数关系用图象表示如下:
的函数关系用图象表示如下:

则上述四个函数图象中,甲、乙两人运行的函数关系的图象应该分别是( )
A. 图①、图② B. 图①、图④ C. 图③、图② D. 图③、图④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一片森林原面积为![]() .计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的
.计划从某年开始,每年砍伐一些树林,且每年砍伐面积的百分比相等.并计划砍伐到原面积的一半时,所用时间是10年.为保护生态环境,森林面积至少要保留原面积的![]() .已知到今年为止,森林剩余面积为原面积的
.已知到今年为止,森林剩余面积为原面积的![]() .
.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)为保护生态环境,今后最多还能砍伐多少年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,以
两点,以![]() 为对角线作正方形
为对角线作正方形![]() ,记直线
,记直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,问
,问![]() 、
、![]() 两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌汽车的![]() 店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
店,对最近100份分期付款购车情况进行统计,统计情况如下表所示.已知分9期付款的频率为0.4;该店经销一辆该品牌汽车,若顾客分3期付款,其利润为1万元;分6期或9期付款,其利润为2万元;分12期付款,其利润为3万元.
付款方式 | 分3期 | 分6期 | 分9期 | 分12期 |
频数 | 20 | 20 |
|
|
(1)若以上表计算出的频率近似替代概率,从该店采用分期付款购车的顾客(数量较大)中随机抽取3为顾客,求事件![]() :“至多有1位采用分6期付款“的概率
:“至多有1位采用分6期付款“的概率![]() ;
;
(2)按分层抽样方式从这100为顾客中抽取5人,再从抽取的5人中随机抽取3人,记该店在这3人身上赚取的总利润为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com