
| 1 |
| 4 |
| 1 |
| 2 |
 借助于图形来看四个选项,先利用f(
借助于图形来看四个选项,先利用f(| 1 |
| 4 |
| 1 |
| 2 |
 解:如图,因为在以为圆心,为半径的圆上运动,对于①当=
解:如图,因为在以为圆心,为半径的圆上运动,对于①当=| 1 |
| 4 |
| 1 |
| 2π |
| 1 |
| 2π |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
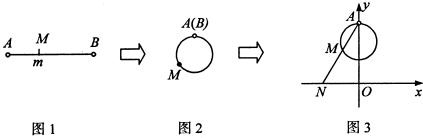
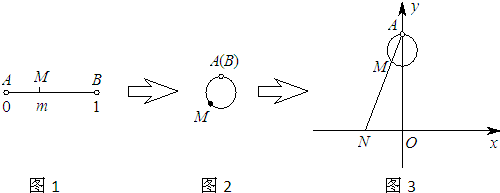
 下图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图1),将线段AB围成一个正方形,使两端点A,B恰好重合(如图2),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图3),若图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.
下图展示了一个由区间(0,4)到实数集R的映射过程:区间(0,4)中的实数m对应数轴上的点M(如图1),将线段AB围成一个正方形,使两端点A,B恰好重合(如图2),再将这个正方形放在平面直角坐标系中,使其中两个顶点在y轴上,点A的坐标为(0,4)(如图3),若图3中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省福州市高三第五次质量检测文科数学 题型:填空题
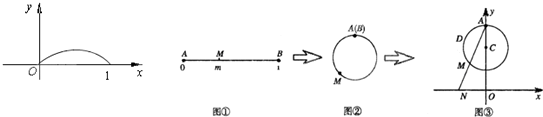
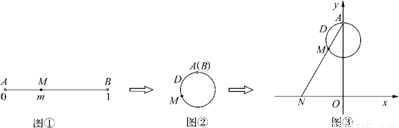
下图展示了一个由区间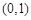 到实数集R的映射过程:区间
到实数集R的映射过程:区间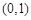 中的实数m对应数轴上的点M,如图①;将线段
中的实数m对应数轴上的点M,如图①;将线段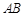 围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为
围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为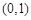 ,在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③中直线
,在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③.图③中直线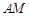 与x轴交于点
与x轴交于点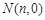 ,则m的象就是n,记作
,则m的象就是n,记作 .
.
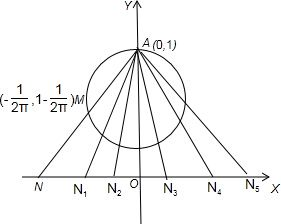
给出下列命题:① ;②
;②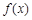 是偶函数;③
是偶函数;③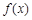 在定义域上单调递增;④
在定义域上单调递增;④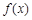 的图象关于点
的图象关于点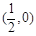 对称,则所有真命题的序号是_______.(填出所有真命题的序号)
对称,则所有真命题的序号是_______.(填出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com