
本小题满分10分)设函数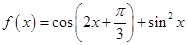 ,
,
(Ⅰ)求函数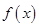 的最大值和最小正周期.,
的最大值和最小正周期.,
(Ⅱ)设A,B,C为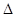 ABC的三个内角,若
ABC的三个内角,若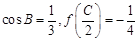 ,且C为锐角,求
,且C为锐角,求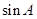
(1)f(x)的最大值为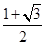 ,最小正周期
,最小正周期 .
.
(2)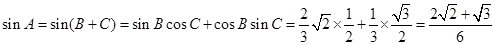
解析试题分析:(1)首先利用二倍角公式化为单一函数,求解最值。
(2)在第一问的基础上,进一步利用同角关系得到B的正弦值和余弦值,然后结合内角和定理,运用 求解得到。
求解得到。
解: (1)f(x)=cos(2x+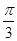 )+sin
)+sin x.=
x.=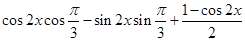
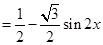 所以函数f(x)的最大值为
所以函数f(x)的最大值为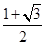 ,最小正周期
,最小正周期 .
.
(2)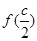 =
=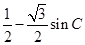 =-
=-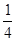 , 所以
, 所以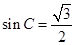 , 因为C为锐角, 所以
, 因为C为锐角, 所以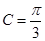 ,
,
又因为在 ABC 中, cosB=
ABC 中, cosB= , 所以
, 所以 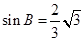 ,
,
所以
考点:本试题主要考查了三角函数的图像与性质的运用。
点评:解决该试题的关键是将函数化为单一函数,结合三角函数的性质得到其最值和周期,统统是结合三角形中同角关系式和两角和差的公式能得到解三角形。


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源: 题型:解答题
(本题满分13 分)
据气象部门预报,在距离某码头南偏东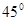 方向600km处的热带风暴中心,正以每小时20km的速度向正北方向移动,距风暴中心450km以内的地区都将受到影响,从现在起多长时间后,该码头将受到热带风暴中心的影响,影响多长时间?(精确到0.1h)
方向600km处的热带风暴中心,正以每小时20km的速度向正北方向移动,距风暴中心450km以内的地区都将受到影响,从现在起多长时间后,该码头将受到热带风暴中心的影响,影响多长时间?(精确到0.1h)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分13分)我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知CD=6 ,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)在锐角三角形ABC中,已知角A、B、C所对的边分别为a、b、c,且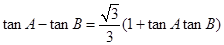 ,
,
(1)若c2=a2+b2—ab,求角A、B、C的大小;
(2)已知向量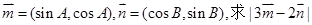 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com