
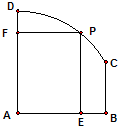
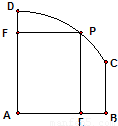
 如图所示的镀锌铁皮材料ABCD,上沿DC为圆弧,其圆心为A,圆半径为2米,AD⊥AB,BC⊥AB,且BC=1米.现要用这块材料裁一个矩形PEAF(其中P在圆弧DC上、E在线段AB上,F在线段AD上)做圆柱的侧面,若以PE为母线,问如何裁剪可使圆柱的体积最大?其最大值是多少?
如图所示的镀锌铁皮材料ABCD,上沿DC为圆弧,其圆心为A,圆半径为2米,AD⊥AB,BC⊥AB,且BC=1米.现要用这块材料裁一个矩形PEAF(其中P在圆弧DC上、E在线段AB上,F在线段AD上)做圆柱的侧面,若以PE为母线,问如何裁剪可使圆柱的体积最大?其最大值是多少? 解法1:分别以AB、AD所在直线为x轴、y轴建立直角坐标系xoy,
解法1:分别以AB、AD所在直线为x轴、y轴建立直角坐标系xoy, ,
, ,圆柱半径为r,体积为V,则
,圆柱半径为r,体积为V,则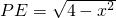 ,
, ,
,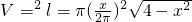 =
=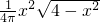 ,
,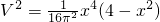 ,
, ,
, ,
, 时,u'<0,u是减函数;当
时,u'<0,u是减函数;当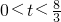 时,u'>0,u是增函数,
时,u'>0,u是增函数, 时,u有极大值,也是最大值,
时,u有极大值,也是最大值,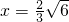 米时,V有最大值
米时,V有最大值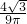 米3,此时
米3,此时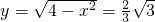 米,
米,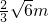 和
和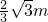 ,能使圆柱的体积最大,其最大值为
,能使圆柱的体积最大,其最大值为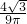 m3.
m3.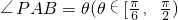 ,则PE=2sinθ,AE=2cosθ,
,则PE=2sinθ,AE=2cosθ, ,
, ,
,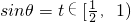 ,u=t(1-t2),
,u=t(1-t2),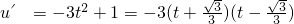 ,
,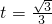 ,
, 时,u'<0,u是减函数;当
时,u'<0,u是减函数;当 时,u'>0,u是增函数,
时,u'>0,u是增函数,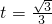 时,u有极大值,也是最大值.
时,u有极大值,也是最大值. 时,V有最大值
时,V有最大值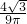 米3.
米3. ,圆柱半径为r,体积为V,则
,圆柱半径为r,体积为V,则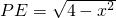 ,
, ,从而可求体积,利用换元法,结合求导数,即可求得V的最大值;
,从而可求体积,利用换元法,结合求导数,即可求得V的最大值;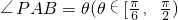 ,则PE=2sinθ,AE=2cosθ,
,则PE=2sinθ,AE=2cosθ, ,从而可求体积,利用换元法,结合求导数,即可求得V的最大值.
,从而可求体积,利用换元法,结合求导数,即可求得V的最大值.

 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
 (2012•扬州模拟)如图所示的镀锌铁皮材料ABCD,上沿DC为圆弧,其圆心为A,圆半径为2米,AD⊥AB,BC⊥AB,且BC=1米.现要用这块材料裁一个矩形PEAF(其中P在圆弧DC上、E在线段AB上,F在线段AD上)做圆柱的侧面,若以PE为母线,问如何裁剪可使圆柱的体积最大?其最大值是多少?
(2012•扬州模拟)如图所示的镀锌铁皮材料ABCD,上沿DC为圆弧,其圆心为A,圆半径为2米,AD⊥AB,BC⊥AB,且BC=1米.现要用这块材料裁一个矩形PEAF(其中P在圆弧DC上、E在线段AB上,F在线段AD上)做圆柱的侧面,若以PE为母线,问如何裁剪可使圆柱的体积最大?其最大值是多少?查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省扬州市高三(下)第三次调研数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com