
分析 由题意作平面区域,建立向量$\overrightarrow{OA}$=(1,1),$\overrightarrow{OP}$=(x,y),从而可得OP•cos∠AOP=$\frac{\overrightarrow{OA}•\overrightarrow{OP}}{|\overrightarrow{OA}|}$=$\frac{x+y}{\sqrt{2}}$,从而解得.
解答 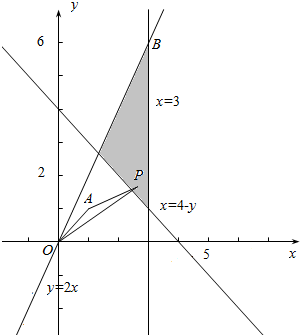 解:由题意作平面区域如下,
解:由题意作平面区域如下,
,
设$\overrightarrow{OA}$=(1,1),$\overrightarrow{OP}$=(x,y),
则OP•cos∠AOP=$\frac{\overrightarrow{OA}•\overrightarrow{OP}}{|\overrightarrow{OA}|}$=$\frac{x+y}{\sqrt{2}}$,
结合图象可知,4≤x+y≤9,
∴2$\sqrt{2}$≤$\frac{x+y}{\sqrt{2}}$≤$\frac{9\sqrt{2}}{2}$,
故答案为:[2$\sqrt{2}$,$\frac{9\sqrt{2}}{2}$].
点评 本题考查了线性规划与向量的综合应用.


科目:高中数学 来源: 题型:选择题
| A. | 经过点(1,2)垂直x轴的直线 | B. | 经过点(1,2)垂直y轴的直线 | ||
| C. | 经过点(2,1)垂直x轴的直线 | D. | 经过点(2,1)垂直y轴的直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
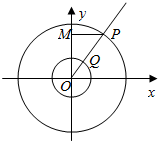 如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.
如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com