
分析 (1)若函数f(x)有零点,则△=16a2-4(2a+6)<0,解得答案;
(2)在(1)的条件下,求g(a)=-a2-3a+2,a∈(-1,$\frac{3}{2}$),结合二次函数的图象和性质,可得函数的值域.
解答 解:(1)若函数f(x)有零点,
则△=16a2-4(2a+6)<0,
解得:a∈(-1,$\frac{3}{2}$);
(2)在(1)的条件下,求g(a)=2-a•|a+3|=-a2-3a+2,a∈(-1,$\frac{3}{2}$);
∵g(a)=-a2-3a+2的图象是开口朝下,且以直线x=-$\frac{3}{2}$为对称轴的抛物线,
故当a∈(-1,$\frac{3}{2}$)时,函数为减函数,
故当a=-1时,函数取最大值4,当a=$\frac{3}{2}$时,函数取最小值-$\frac{19}{4}$,
故g(a)=2-a•|a+3|的值域为(-$\frac{19}{4}$,4)
点评 本题考查的知识点是二次函数的性质,函数的零点,函数的值域,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
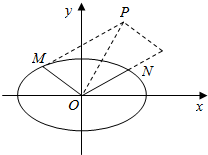 如图所示,已知M,N是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上两动点,且直线OM与ON的斜率之积为-$\frac{1}{2}$(其中O为坐标原点),若点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$.问:是否存在两个定点F1,F2,使得|PF1|+|PF2|为定值.若存在,求F1,F2的坐标;若不存在,说明理由.
如图所示,已知M,N是椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}$=1上两动点,且直线OM与ON的斜率之积为-$\frac{1}{2}$(其中O为坐标原点),若点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$.问:是否存在两个定点F1,F2,使得|PF1|+|PF2|为定值.若存在,求F1,F2的坐标;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
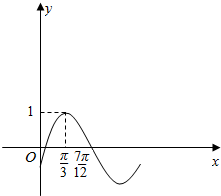 函数f(x)=sin(ωx+φ)(ω>0.|φ|<$\frac{π}{2}$)的图象部分如图所示.
函数f(x)=sin(ωx+φ)(ω>0.|φ|<$\frac{π}{2}$)的图象部分如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com