
选修4-1几何证明选讲,如图,D,E分别是AB,AC边上的点,且不与顶点重合,已知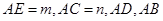 为方程
为方程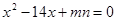 的两根,
的两根,
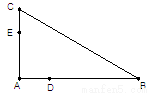
(1) 证明 C,B,D,E四点共圆;
(2)若 ,求C,B,D,E四点所在圆的半径。
,求C,B,D,E四点所在圆的半径。
(1)见解析(2)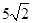
【解析】本试题主要是考查了四点共圆的证明以及圆的半径的求解综合运用。
(1)由于连接DE,根据题意在△ADE和△ACB中,结合根与系数的关系可知△ADE∽△ACB,那么因此 ∠ADE=∠ACB , 所以C,B,D,E四点共圆。
(2)m=4, n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
结合平行关系得到结论。
解:(I)连接DE,根据题意在△ADE和△ACB中,
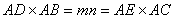
即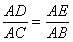 .又∠DAE=∠CAB,从而△ADE∽△ACB
因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
.又∠DAE=∠CAB,从而△ADE∽△ACB
因此∠ADE=∠ACB , 所以C,B,D,E四点共圆。
(Ⅱ)m=4, n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故 AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=900,故GH∥AB, HF∥AC.
HF=AG=5,DF= 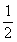 (12-2)=5.
(12-2)=5.
故C,B,D,E四点所在圆的半径为5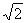


科目:高中数学 来源: 题型:
 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)| 192 |
| 25 |
| 192 |
| 25 |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (选修4-1几何证明选讲)
(选修4-1几何证明选讲)查看答案和解析>>
科目:高中数学 来源: 题型:
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)| π |
| 4 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| x+2y |
| xy |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com