
分析 把已知等式两边平方,求得x+x-1,再平方求得x2+x-2,代入要求的代数式得答案.
解答 解:∵${x^{\frac{1}{2}}}+{x^{-\frac{1}{2}}}=3$,
∴$({x}^{\frac{1}{2}}+{x}^{-\frac{1}{2}})^{2}=9$,得x+x-1=7,
两边再平方得(x+x-1)2=49,∴x2+x-2=47.
则$\frac{{x+{x^{-1}}+3}}{{{x^2}+{x^{-2}}-2}}$=$\frac{7+3}{47-2}=\frac{2}{9}$.
故答案为:$\frac{2}{9}$.
点评 本题考查有理指数幂的化简求值,考查有理指数幂的运算性质,是基础的计算题.


科目:高中数学 来源: 题型:解答题
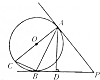 如图,AC是圆O的直径,AC=4,PA,PB是圆O的切线,A,B为其切点,过A作AD⊥BP,交BP于D点,连接AB、BC.
如图,AC是圆O的直径,AC=4,PA,PB是圆O的切线,A,B为其切点,过A作AD⊥BP,交BP于D点,连接AB、BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 12 | C. | -12 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com