
已知a、b、c分别是△ABC三个内角A、B、C的对边.
(1)若△ABC面积为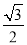 ,c=2,A=60º,求a,b的值;
,c=2,A=60º,求a,b的值;
(2)若acosA=bcosB,试判断△ABC的形状,证明你的结论.
(1)a= ,b=1,(2)直角三角形或等腰三角形
,b=1,(2)直角三角形或等腰三角形
【解析】
试题分析:(1)解三角形问题,一般利用正余弦定理进行边角转化.由面积公式有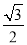 =
= bcsinA=bsin60º,∴b=1.再由余弦定理a2=b2+c2-2bccosA=3,∴a=
bcsinA=bsin60º,∴b=1.再由余弦定理a2=b2+c2-2bccosA=3,∴a= .(2)由正弦定理得2RsinA=a,2RsinB=b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B为三角形内角,∴A+B=90º或A=B.∴△ABC为直角三角形或等腰三角形.本题也可从余弦定理出发:
.(2)由正弦定理得2RsinA=a,2RsinB=b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B为三角形内角,∴A+B=90º或A=B.∴△ABC为直角三角形或等腰三角形.本题也可从余弦定理出发: 所以
所以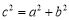 或
或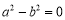 .
.
【解析】
(1)由已知得 =
= bcsinA=bsin60º,∴b=1.
bcsinA=bsin60º,∴b=1.
由余弦定理a2=b2+c2-2bccosA=3,∴a= .
.
(2)由正弦定理得2RsinA=a,2RsinB=b,
∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,由已知A、B为三角形内角,
∴A+B=90º或A=B.∴△ABC为直角三角形或等腰三角形
考点:正余弦定理


科目:高中数学 来源:2016届江苏省高一下学期期中考试数学试卷(解析版) 题型:解答题
已知数列{an}是等差数列,数列{bn}是等比数列,且对任意的n∈N*,都有a1b1+a2b2+a3b3+···+anbn=n·2n+3.
(1)若{bn}的首项为4,公比为2,求数列{an+bn}的前n项和Sn;
(2)若a1=8.
①求数列{an}与{bn}的通项公式;
②试探究:数列{bn}中是否存在某一项,它可以表示为该数列中其它r(r∈N,r≥2)项的和?若存在,请求出该项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高一下学期期中考试数学试卷(解析版) 题型:填空题
设等差数列{an}的前n项的和为Sn,若a1>0,S4=S8,则当Sn取最大值时,n的值为____________.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省徐州市高一下学期期末模拟数学试卷3(解析版) 题型:填空题
如图,为了测定河的宽度,在一岸边选定两点A,B和对岸标记物C,测得∠CAB=30°,∠CBA=45°,AB=120 m,则河的宽度为 m.
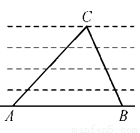
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com