
【题目】下列命题中,正确的个数是( )
①直线上有两个点到平面的距离相等,则这条直线和这个平面平行;
②![]() 为异面直线,则过
为异面直线,则过![]() 且与
且与![]() 平行的平面有且仅有一个;
平行的平面有且仅有一个;
③直四棱柱是直平行六面体;
④两相邻侧面所成角相等的棱锥是正棱锥.
A.0B.1C.2D.3
【答案】B
【解析】
①可通过点分居平面两侧来进行否定;
②利用异面直线的性质与线面平行的判定即可判断出②正确;
③通过直四棱柱和直平行六面体定义来进行否定;
④通过把正方形折叠的方式可找到反例来进行否定.
①中,两点可分别位于平面的两侧,存在到平面距离相等的情况,此时直线和平面相交
①错误;
②中,作![]() 的平行线
的平行线![]() ,且
,且![]() 与
与![]() 交于一点;则由
交于一点;则由![]() 可确定唯一的平面
可确定唯一的平面![]() ,此时
,此时![]() ,可知这样的平面有且仅有一个,②正确;
,可知这样的平面有且仅有一个,②正确;
③中,直四棱柱为底面为四边形,侧棱垂直于底面的四棱柱;直平行六面体是底面为平行四边形,且侧棱垂直于底面的四棱柱;③错误;
④中,若正方形一个顶点为![]() ,
,![]() 为两边的中点,如下图所示:
为两边的中点,如下图所示:
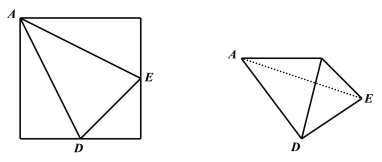
将正方形沿![]() 三边折叠为三棱锥,满足两相邻侧面所成角相等,但不是正三棱锥
三边折叠为三棱锥,满足两相邻侧面所成角相等,但不是正三棱锥
④错误
故选:![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
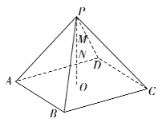
【题目】如图,在四棱锥![]() 中,顶点P在底面的投影
中,顶点P在底面的投影![]() 恰为正方形ABCD的中心且
恰为正方形ABCD的中心且![]() ,设点M,N分别为线段PD,PO上的动点,已知当
,设点M,N分别为线段PD,PO上的动点,已知当![]() 取得最小值时,动点M恰为PD的中点,则该四棱锥的外接球的表面积为____________.
取得最小值时,动点M恰为PD的中点,则该四棱锥的外接球的表面积为____________.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由满足下列性质的函数
是由满足下列性质的函数![]() 构成的集合:在函数
构成的集合:在函数![]() 的定义城内存在
的定义城内存在![]() ,使得
,使得![]() 成立,已知下列函数:①
成立,已知下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() . 其中属于集合
. 其中属于集合![]() 的函数是________. (写出所有满足要求的函数的序号)
的函数是________. (写出所有满足要求的函数的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午佳节旌旗胜,龙舟竞渡展雄风.端午龙舟竞渡活动是我国的民间传统习俗,龙舟精神激发着汕尾海陆丰老区人民敢为人先、奋发有为的勇气.每年在粽叶飘香的端午节到来的前一天,汕尾市都将在美丽的品清湖畔举行龙舟锦标赛,他们将在这片碧蓝的品清湖上挥桨劈浪,奋勇争先,一往无前的龙舟精神,该活动也为市民提供了难得的视觉盛宴.某商家为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了6月2日至6月6日的白天平均气温![]() (℃)与该奶茶店的这种饮料销量
(℃)与该奶茶店的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日期 | 6月2日 | 6月3日 | 6月4日 | 6月5日 | 6月6日 |
平均气温 | 27 | 29 | 31 | 30 | 33 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出了![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;若气象台预报6月7日白天的平均气温为35℃,根据线性回归方程预测该奶茶店这种饮料的销量(取整数).
;若气象台预报6月7日白天的平均气温为35℃,根据线性回归方程预测该奶茶店这种饮料的销量(取整数).
附:线性回归方程![]() 中,
中,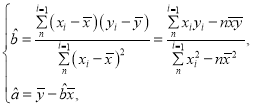 其中
其中![]() ,
,![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年“非洲猪瘟”过后,全国生猪价格逐步上涨,某大型养猪企业,欲将达到养殖周期的生猪全部出售,根据去年的销售记录,得到销售生猪的重量的频率分布直方图(如图所示).

(1)根据去年生猪重量的频率分布直方图,估计今年生猪出栏(达到养殖周期)时,生猪重量达不到270斤的概率(以频率代替概率);
(2)若假设该企业今年达到养殖周期的生猪出栏量为5000头,生猪市场价格是30元/斤,试估计该企业本养殖周期的销售收入是多少万元;
(3)若从本养殖周期的生猪中,任意选两头生猪,其重量达到270斤及以上的生猪数为随机变量![]() ,试求随机变量
,试求随机变量![]() 的分布列及方差.
的分布列及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() (
(![]() )左,右焦点分别为
)左,右焦点分别为![]() ,
,![]() ,且椭圆的长轴长为
,且椭圆的长轴长为![]() ,右准线方程为
,右准线方程为![]() .
.
(1)求椭圆C的方程;
(2)设直线l过椭圆C的右焦点![]() ,且与椭圆相交与A,B(与左右顶点不重合)
,且与椭圆相交与A,B(与左右顶点不重合)
(i)椭圆的右顶点为M,设![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,求
,求![]() 的值;
的值;
(ii)若椭圆上存在一点D满足![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的最小值是
的最小值是![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)已知动直线![]() 与圆
与圆![]() :
:![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() ,
,![]() 两点.是否存在实数
两点.是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com