练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    过点A（2，1）的直线交圆x2+y2-2x+4y=0于B，C两点，当|BC|最大时，直线BC的方程是（　　）
    A、3x-y-5=0B、3x+y-7=0C、x+3y-5=0D、x-3y+5=0
    分析：设出直线BC的方程为y=kx+b，由题意可知当|BC|最大时，过A的直线必然过圆的圆心，故把圆的方程化为标准方程，找出圆心的坐标，再由A的坐标，都代入到所设的方程中求出k和b的值，从而确定出直线BC的方程．
    解答：解：把圆的方程x2+y2-2x+4y=0化为标准方程为（x-1）2+（y+2）2=5，
    ∴圆心坐标为（1，-2），
    设直线BC的方程为y=kx+b，又A（2，1），
    把圆心坐标和A的坐标代入得：
    2k+b=1
    k+b=-2
    ，
    解得
    k=3
    b=-5
    ，
    则直线BC的方程为y=3x-5，即3x-y-5=0．
    故选A
    点评：此题考查了直线与圆相交的性质，以及根据两点坐标利用待定系数法求直线的解析式，理解|BC|最大即线段BC为圆的直径，即直线BC过圆心是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图梯形ABCD，AD∥BC，∠A=90°，过点C作CE∥AB，AD=2BC，AB=BC，，现将梯形沿CE折成直二面角D-EC-AB．
    （1）求直线BD与平面ABCE所成角的正切值；
    （2）设线段AB的中点为P，在直线DE上是否存在一点M，使得PM∥面BCD？若存在，请指出点M的位置，并证明你的结论；若不存在，请说明理由；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

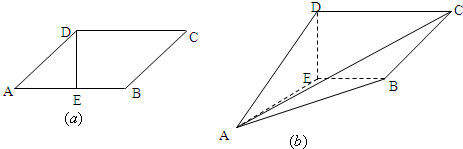    已知边长为2的菱形ABCD，如图（a）所示，∠BAD=60°，过D点作DE⊥AB于E点，现沿着DE折成一个直二面角，如图（b）所示；
    （1）求AC与BD所成角的余弦值；
    （2）求点D到平面ABC的距离；
    （3）连接CE，在CE上取点G，使EG=
    2
    		7
    7
    ，连接BG，求证：AC⊥BG．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    椭圆E：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）离心率为
    		3
    2
    ，且过P（
    		6
    ，
    		2
    2
    ）．
    （1）求椭圆E的方程；
    （2）已知直线l过点M（-
    1
    2
    ，0），且与开口朝上，顶点在原点的抛物线C切于第二象限的一点N，直  线l与椭圆E交于A，B两点，与y轴交与D点，若
    AB
    =λ
    AN
    ，
    BD
    =μ
    BN
    ，且λ+μ=
    5
    2
    ，求抛物线C的标准方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，在直三棱柱ABC-A′B′C′中，点D是BC的中点，∠ACB=90°，AC=BC=1，AA′=2，
    （1）欲过点A′作一截面与平面AC'D平行，问应当怎样画线，写出作法，并说明理由；
    （2）求异面直线BA′与 C′D所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年安徽省皖南八校高三第一次联考理科数学试卷 题型：解答题

    （本小题满分12分）已知椭圆过点A（a,0）,B(0,b)的直

     

    线倾斜角为，原点到该直线的距离为.

     

    （1）求椭圆的方程；

    （2）斜率小于零的直线过点D（1，0）与椭圆交于M，N两点，若求直线MN的方程；

    （3）是否存在实数k，使直线交椭圆于P、Q两点，以PQ为直径的圆过点D（1，0）？若存在，求出k的值；若不存在，请说明理由。

     

    查看答案和解析>>

    同步练习册答案