一个口袋中装有大小相同的n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖.
(1)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为P.试问当n等于多少时,P的值最大?
(2)在(1)的条件下,将5个白球全部取出后,对剩下的n个红球全部作如下标记:记上i号的有i个(i=1,2,3,4),其余的红球记上0号,现从袋中任取一球.ξ表示所取球的标号,求ξ的分布列,期望和方差.
【答案】
分析:(1)计算出从n+5个球中任取两个的方法数和其中两个球的颜色不同的方法,由古典概型公式,代入数据得到一次摸奖中奖的概率,再利用函数的单调性求出其最大值及相应的p值即可.
(2)所取球的标号为ξ,由题意知ξ的取值是0、1、2、3,4.本题是一个独立重复试验,根据上面的p值,代入公式得到结果,写出分布列,期望和方差.
解答:解:(1)一次摸奖从n+5个球中任取两个,有C
n+52种方法.它们是等可能的,其中两个球的颜色不同的方法有C
n1C
51种,
一次摸奖中奖的概率P=

…(2分)
设每次摸奖中奖的概率为p(0<p<1),三次摸奖中(每次摸奖后放回)恰有一次中奖的概率,
P=

=3p
3-6p
2+3p
∴P′=9p
2-12p+3=3(p-1)(3p-1),
由此知P在

上为增函数,P在
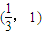
上为减函数,…(4分)
∴当
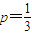
时P取得最大值,即
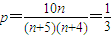
,
解得n=20或n=1(舍去),则当n=20时,三次摸奖(每次摸奖后放回)恰有一次中奖的概率最大.…(6分)
(2)由(1)可知:记上0号的有10个红球,从中任取一球,有20种取法,它们是等可能的故ξ的分布列是
…(8分)
Eξ=0×

+1×

+2×

+3×

+4×

=

…(10分)
Dξ=(0-

)
2×

+(1-

)
2×
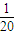
+(2-

)
2×
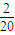
+(3-

)
2×

+(4-

)
2×

=

…(12分)
点评:本小题主要考查函数单调性的应用、等可能事件的概率、离散型随机变量的期望与方差等基础知识,求离散型随机变量期望的步骤:①确定离散型随机变量 的取值.②写出分布列,并检查分布列的正确与否,即看一下所有概率的和是否为1.③求出期望.

 …(2分)
…(2分) =3p3-6p2+3p
=3p3-6p2+3p 上为增函数,P在
上为增函数,P在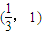 上为减函数,…(4分)
上为减函数,…(4分)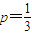 时P取得最大值,即
时P取得最大值,即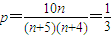 ,
,




 +1×
+1× +2×
+2× +3×
+3× +4×
+4× =
= …(10分)
…(10分) )2×
)2× +(1-
+(1- )2×
)2×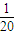 +(2-
+(2- )2×
)2×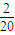 +(3-
+(3- )2×
)2× +(4-
+(4- )2×
)2× =
= …(12分)
…(12分)
