
【题目】如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程. 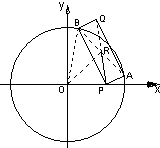
【答案】解:设AB的中点为R,则R也是PQ的中点,设R的坐标为(x1 , y1),则在Rt△ABP中,|AR|=|PR|.
又因为R是弦AB的中点,依垂径定理:在Rt△OAR中,|AR|2=|AO|2﹣|OR|2=36﹣( ![]() ).
).
又|AR|=|PR|= ![]() ,所以有(x1﹣4)2+
,所以有(x1﹣4)2+ ![]() =36﹣(
=36﹣( ![]() ),即
),即 ![]() ﹣4x1﹣10=0.
﹣4x1﹣10=0.
因此点R在一个圆上,而当R在此圆上运动时,Q点即在所求的轨迹上运动.
设Q(x,y),因为R是PQ的中点,所以x1= ![]() ,
,
代入方程 ![]() ﹣4x1﹣10=0,得
﹣4x1﹣10=0,得 ![]() ﹣10=0,
﹣10=0,
整理得:x2+y2=56,这就是所求的Q点的轨迹方程.
【解析】设AB的中点为R,设R的坐标为(x1 , y1),则在Rt△ABP中,|AR|=|PR|,在Rt△OAR中,|AR|2=|AO|2﹣|OR|2=36﹣( ![]() ),再由|AR|=|PR|=
),再由|AR|=|PR|= ![]() ,由此得到点R的轨迹方程
,由此得到点R的轨迹方程 ![]() ﹣4x1﹣10=0①,设Q(x,y),因为R是PQ的中点,可得x1=
﹣4x1﹣10=0①,设Q(x,y),因为R是PQ的中点,可得x1= ![]() ,代入①化简即得所求.
,代入①化简即得所求.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在数列{an}中,a3=12,a11=﹣5,且任意连续三项的和均为11,则a2017=;设Sn是数列{an}的前n项和,则使得Sn≤100成立的最大整数n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱 ![]() 中,底面
中,底面 ![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段 ![]() ,
, ![]() 的中点.
的中点.
(1)求证: ![]() ||平面
||平面 ![]() ;
;
(2)四棱柱 ![]() 的外接球的表面积为
的外接球的表面积为 ![]() ,求异面直线
,求异面直线 ![]() 与
与 ![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点. 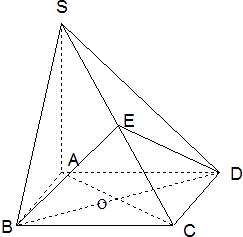
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
(3)设SA=4,AB=2,当OE丄SC时,求二面角E﹣BD﹣C余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x),满足f(1﹣x)=f(x),(x﹣ ![]() )f′(x)>0,若x1<x2且x1+x2>1,则有( )
)f′(x)>0,若x1<x2且x1+x2>1,则有( )
A.f(x1)<f(x2)
B.f(x1)>f(x2)
C.f(x1)=f(x2)
D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)是定义在(0,+∞)上的函数,当x>1时,f(x)>0,且满足 ![]() .
.
(1)求f(1)的值;
(2)判断并证明函数的单调性;
(3)若f(2)=1,解不等式 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com