
【题目】某公司租赁甲、乙两种设备生产![]() 、
、![]() 两类产品,甲种设备每天能生产
两类产品,甲种设备每天能生产![]() 类产品
类产品![]() 件和
件和![]() 类产品
类产品![]() 件,乙种设备每天能生产
件,乙种设备每天能生产![]() 类产品
类产品![]() 件和
件和![]() 类产品
类产品![]() 件.已知设备甲每天的租赁费为
件.已知设备甲每天的租赁费为![]() 元,设备乙每天的租赁费为
元,设备乙每天的租赁费为![]() 元,现该公司至少要生产
元,现该公司至少要生产![]() 类产品
类产品![]() 件,
件,![]() 类产品
类产品![]() 件,求所需租赁费最少为多少元?
件,求所需租赁费最少为多少元?
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某市教育局卫生健康所对全市高三年级的学生身高进行抽样调查,随机抽取了100名学生,他们身高都处于![]() 五个层次,根据抽样结果得到如下统计图表,则从图表中不能得出的信息是( )
五个层次,根据抽样结果得到如下统计图表,则从图表中不能得出的信息是( )
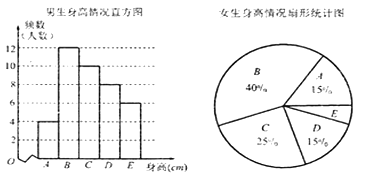
A. 样本中男生人数少于女生人数
B. 样本中![]() 层次身高人数最多
层次身高人数最多
C. 样本中![]() 层次身高的男生多于女生
层次身高的男生多于女生
D. 样本中![]() 层次身高的女生有3人
层次身高的女生有3人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知位于![]() 轴左侧的圆
轴左侧的圆![]() 与
与![]() 轴相切于点
轴相切于点![]() 且被
且被![]() 轴分成的两段圆弧长之比为
轴分成的两段圆弧长之比为![]() ,直线
,直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() .
.

(1)求圆![]() 的方程;
的方程;
(2)求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过右焦点
,过右焦点![]() 任作一条不垂直于坐标轴的直线l与椭圆C交于A,B两点,
任作一条不垂直于坐标轴的直线l与椭圆C交于A,B两点,![]() 的周长为
的周长为![]() .
.
(1)求椭圆C的方程;
(2)记点B关于x轴的对称点为![]() 点,直线
点,直线![]() 交x轴于点D.求
交x轴于点D.求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆C1:x2+y2﹣10x+4y+25=0与圆C2:x2+y2﹣14x+2y+25=0,点A,B分别是C1,C2上的动点,M为直线y=x上的动点,则|MA|+|MB|的最小值为( )
A.3![]() B.3
B.3![]() C.5
C.5![]() D.5
D.5![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体中,四边形![]() 为菱形,对角线
为菱形,对角线![]() 与
与![]() 的交点为
的交点为![]() ,四边形
,四边形![]() 为梯形,
为梯形,![]() ,
,![]() .
.
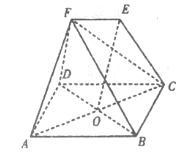
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若![]() ,求
,求![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点下的距离为10.
到其焦点下的距离为10.
(1)求抛物线C的方程;
(2)设过焦点F的的直线![]() 与抛物线C交于
与抛物线C交于![]() 两点,且抛物线在
两点,且抛物线在![]() 两点处的切线分别交x轴于
两点处的切线分别交x轴于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一块黄铜板上插着三根宝石针,在其中一根针上从下到上穿好由大到小的若干金片.若按照下面的法则移动这些金片:每次只能移动一片金片;每次移动的金片必须套在某根针上;大片不能叠在小片上面.设移完n片金片总共需要的次数为an,可推得a1=1,an+1=2an+1.如图是求移动次数在1000次以上的最小片数的程序框图模型,则输出的结果是( )
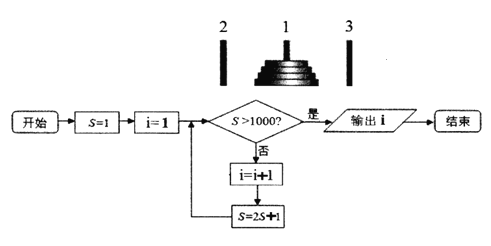
A. 8B. 9C. 10D. 11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com