解:(1)k
AB=y′|
x=p0=

p
0,
直线AB的方程为y-

p
02=

p
0(x-p
0),即y=

p
0x-

p
02,
∴q=

p
0p-

p
02,方程x
2-px+q=0的判别式△=p
2-4q=(p-p
0)
2,
两根x
1,2=

=
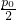
或p-
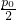
,
而|p-
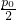
|=||p|-|
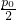
||,又0≤|p|≤|p
0|,
∴
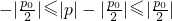
,得|p-
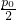
|=||p|-|
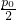
||
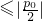
,
∴φ(p,q)=

;
(2)由a
2-4b>0知点M(a,b)在抛物线L的下方,
①当a>0,b≥0时,作图可知,若M(a,b)∈X,则p
1>p
2≥0,
得|p
1|>|p
2|;显然有点M(a,b)∈X;∴M(a,b)∈X?|P
1|<|P
2|.
②当a>0,b<0时,点M(a,b)在第二象限,作图可知,若M(a,b)∈X,则p
1>0>p
2,
且|p
1|>|p
2|;
显然有点M(a,b)∈X,
∴显然有点M(a,b)∈X?|P
1|<|P
2|.
根据曲线的对称性可知,当a<0时,M(a,b)∈X?|P
1|<|P
2|.
综上所述,M(a,b)∈X?|P
1|<|P
2|. (*)
由(1)知点M在直线EF上,方程x
2-ax+b=0的两根x
1,2=
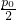
或a-
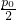
,
同理知点M在直线E′F′上,方程x
2-ax+b=0的两根x
1,2=
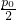
或a-
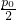
,
若φ(a,b)=
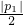
,则
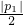
不比|a-
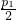
|、
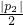
、|a-

|小,
∴|p
1|>|p
2|;又|p
1|>|p
2|?M(a,b)∈X;
∴φ(p,q)=
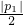
?M(a,b)∈X;
又由(1)知,M(a,b)∈X?φ(p,q)=
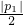
;
∴M(a,b)∈X?φ(p,q)=
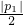
,综合(*)式,得证.
(3)联立y=x-1,y=

(x+1)
2-

得交点(0,-1),(2,1),可知0≤p≤2,
过点(p,q)抛物线L的切线,设切点为(x
0,

x
02),则

,
得x
02-2px
0+4q=0,解得x
0=p+
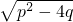
,
又q≥

(p+1)
2-

,即p
2-4q≤4-2p,
x
0≤p+
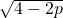
,设
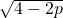
=t,x
0≤
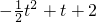
=
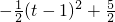
≤

,
∴φ
max=

;
而x
0≥p+
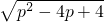
=p+|p-2|=2,
∴φ
min=
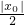
=1.
分析:(1)求导,写出过点A(p
0,

p
02)(p
0≠0)L的切线方程,求得点B的坐标,即可证得结果;
(2)求出过M(a,b)作L的两条切线l
1,l
2,根据φ(p,q)=max{|x
1|,|x
2|},比较
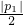
、|a-
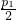
|、
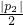
、|a-

|的大小,即可证得结论;
(3)联立y=x-1,y=

(x+1)
2-

求得交点坐标,利用导数求过点(p,q)抛物线L的切线方程,求得切点坐标,转化为求函数的最值问题.
点评:此题是个难题.本题考查了利用导数研究抛物线的切线方程,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.其中问题形式是个新定义问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

 x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}. p02)(p0≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)=
p02)(p0≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)= ;
;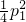 ),E′(p2,
),E′(p2, p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=
p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=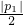 .
. (x+1)2-
(x+1)2- }.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)
}.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax) p0,
p0, p02=
p02= p0(x-p0),即y=
p0(x-p0),即y= p0x-
p0x- p02,
p02, p0p-
p0p- p02,方程x2-px+q=0的判别式△=p2-4q=(p-p0)2,
p02,方程x2-px+q=0的判别式△=p2-4q=(p-p0)2, =
=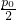 或p-
或p-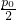 ,
,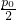 |=||p|-|
|=||p|-|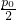 ||,又0≤|p|≤|p0|,
||,又0≤|p|≤|p0|,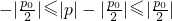 ,得|p-
,得|p-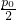 |=||p|-|
|=||p|-|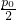 ||
||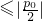 ,
, ;
;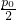 或a-
或a-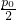 ,
,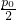 或a-
或a-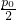 ,
,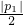 ,则
,则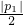 不比|a-
不比|a-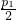 |、
|、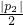 、|a-
、|a- |小,
|小,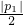 ?M(a,b)∈X;
?M(a,b)∈X;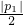 ;
;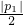 ,综合(*)式,得证.
,综合(*)式,得证. (x+1)2-
(x+1)2- 得交点(0,-1),(2,1),可知0≤p≤2,
得交点(0,-1),(2,1),可知0≤p≤2, x02),则
x02),则 ,
,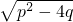 ,
, (p+1)2-
(p+1)2- ,即p2-4q≤4-2p,
,即p2-4q≤4-2p,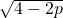 ,设
,设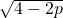 =t,x0≤
=t,x0≤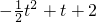 =
=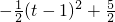 ≤
≤ ,
, ;
;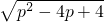 =p+|p-2|=2,
=p+|p-2|=2,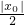 =1.
=1. p02)(p0≠0)L的切线方程,求得点B的坐标,即可证得结果;
p02)(p0≠0)L的切线方程,求得点B的坐标,即可证得结果;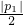 、|a-
、|a-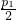 |、
|、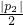 、|a-
、|a- |的大小,即可证得结论;
|的大小,即可证得结论; (x+1)2-
(x+1)2- 求得交点坐标,利用导数求过点(p,q)抛物线L的切线方程,求得切点坐标,转化为求函数的最值问题.
求得交点坐标,利用导数求过点(p,q)抛物线L的切线方程,求得切点坐标,转化为求函数的最值问题.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案![]() .实数p,q满足
.实数p,q满足![]() ,x1,x2是方程
,x1,x2是方程![]() 的两根,记
的两根,记![]() 。
。![]() 作L的切线教y轴于点 B.证明:对线段AB上任一点Q(p,q)有
作L的切线教y轴于点 B.证明:对线段AB上任一点Q(p,q)有![]()
![]() ,切点分别为
,切点分别为![]() ,
,![]() 与y轴分别交与F,F'。线段EF上异于两端点的点集记为X.证明:M(a,b)
与y轴分别交与F,F'。线段EF上异于两端点的点集记为X.证明:M(a,b) ![]() X
X![]()
![]()
![]()
![]()
![]() ;
;![]() (x+1)2-
(x+1)2-![]() }.当点(p,q)取遍D时,求
}.当点(p,q)取遍D时,求![]() 的最小值 (记为
的最小值 (记为![]() )和最大值(记为
)和最大值(记为![]() ).
). x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}. p2)(p≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)=
p2)(p≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)= ;
; ),E′(p2,
),E′(p2, p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=
p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=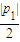 .
. (x+1)2-
(x+1)2- }.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)
}.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)