分析:解法一:
(Ⅰ)欲证明直线与平面垂直,可以先证明直线与直线垂直,由BD⊥CC
1,BD⊥AC可得BD⊥平面ACC
1A
1.
(Ⅱ)先将二面角C
1-BD-C的大小为60°,转化为对应的平面角的大小,根据三垂线定理可知:∠C
1OC∠是二面角C
1-BD-C的平面角,∴∠C
1OC=60°,接着就可以求解异面直线BC
1与AC所成角的大小.求异面直线所成的角,可用几何法,其基本解题思路是“异面化共面,认定再计算”,即利用平移法和补形法将两条异面直线转化到同一个三角形中,结合余弦定理来求.连接A
1B.∵A
1C
1∥AC,∴∠A
1C
1B是BC
1与AC所成的角.
解法二:
在含有直线与平面垂直垂直的条件的棱柱、棱锥、棱台中,也可以建立空间直角坐标系,设定参量求解.这种解法的好处就是:1、解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理,因为这些可以用向量方法来解决.2、即使立体感稍差一些的学生也可以顺利解出,因为只需画个草图以建立坐标系和观察有关点的位置即可.建立空间直角坐标系D-xyz,设AD=a,DD
1=b,则有D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),C
1(0,a,b)
(Ⅰ)、
=(-a,-a,0),=(-a,a,0),=(0,0,b),∴
•=0,•=0,
∴BD⊥AC,BD⊥CC
1,又∵AC,CC
1?平面ACC
1A
1,且AC∩CC
1=C,∴BD⊥平面ACC
1A
1.
(Ⅱ)设BD与AC相交于O,连接C
1O,则点O坐标为
(,,0),=(-,,b),先将二面角C
1-BD-C的大小为60°,转化为对应的平面角的大小,通过计算可知:∠C
1OC∠是二面角C
1-BD-C的平面角,∴∠C
1OC=60°,接着就可以求解异面直线BC
1与AC所成角的大小.

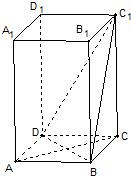 如图,ABCD-A1B1C1D1是正四棱柱.
如图,ABCD-A1B1C1D1是正四棱柱.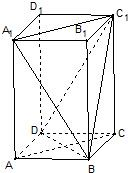 解:法一:
解:法一: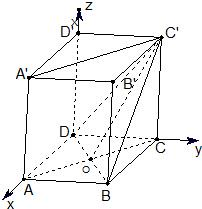 (Ⅱ)设BD与AC相交于O,连接C1O,
(Ⅱ)设BD与AC相交于O,连接C1O,

 学练快车道快乐假期寒假作业系列答案
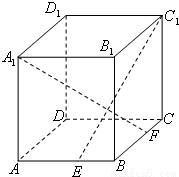
学练快车道快乐假期寒假作业系列答案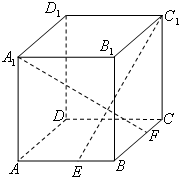 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是