
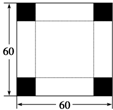
 如图,在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,最大容积是________.
如图,在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,最大容积是________. (60x2-x3)(0<x<60).再用导数工具研究V(x)在区间(0,60)上的单调性,可知当x=40时V(x)达到最大值.由此得到本题答案.
(60x2-x3)(0<x<60).再用导数工具研究V(x)在区间(0,60)上的单调性,可知当x=40时V(x)达到最大值.由此得到本题答案. ,
, (60x2-x3)(0<x<60).
(60x2-x3)(0<x<60). x2,
x2, x2=0,解得x=0(不合题意,舍去),x=40,
x2=0,解得x=0(不合题意,舍去),x=40,

科目:高中数学 来源: 题型:
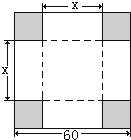 在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,最大容积是
如图,在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,最大容积是查看答案和解析>>
科目:高中数学 来源: 题型:
在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
 |
查看答案和解析>>
科目:高中数学 来源:2014届河南省许昌市五校高二下学期第一次联考理科数学试(解析版) 题型:解答题
在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com