练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知定点在抛物线：（＞0）上，动点且．求证：弦必过一定点．

    【解析】设所在直线方程为：．

    与抛物线方程联立，消去得

    ．

    设，

    则 ……①  

    ……②

    由已知得，．即  ……③

    ∵

    ∴③式可化为，

    即．

    将①②代入得，．

    直线方程化为：．

    ∴直线恒过点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

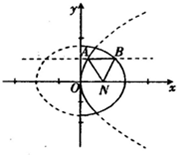    已知定点N（2，0），动点A，B分别在图中抛物线y2=8x及椭圆
    x2
    9
    +
    y2
    5
    =1     的实线部分上运动，且AB∥x轴，则△NAB的周长L的取值范围是
    (
    26
    5
    ，6)
    (
    26
    5
    ，6)
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知定点A（7，12）和抛物线y2=8x，动点P在抛物线上运动，M为P在抛物线准线上的射影，则|PM|+|PA|的最小值为（　　）

    查看答案和解析>>

    科目：高中数学 来源：辽宁省大连市2009-2010学年高一下学期期末考试（数学文）doc 题型：填空题

    已知定点和抛物线的焦点F，在抛物线上求一点P使|PM|+|PF|的值最小，则点的坐标是。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题正确的是

    ①到两个定点的距离之比为常数的动点的轨迹是圆．

    ②椭圆．

    ③双曲线的焦点到渐近线的距离为．

    ④已知点在抛物线上，且,则．

    A．②③④        B．①④        C．①②③        D．①③

    查看答案和解析>>

    同步练习册答案