
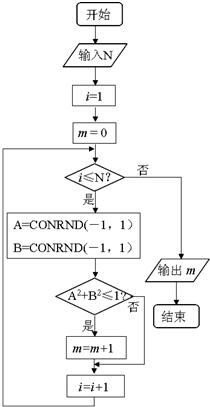
 程序框图可用来估计圆周率π的值.设CONRND(-1,1)是产生随机数的函数,能随机产生区间(-1,1)内的任何一个数,如果输入1000,输出的结果为786,则运用此方法,计算π的近似值为( )
程序框图可用来估计圆周率π的值.设CONRND(-1,1)是产生随机数的函数,能随机产生区间(-1,1)内的任何一个数,如果输入1000,输出的结果为786,则运用此方法,计算π的近似值为( )| 786 |
| 1000 |
| π |
| 4 |
| S圆 |
| S正方形 |
| π |
| 4 |
| m |
| i |
| 786 |
| 1000 |
| π |
| 4 |
| 786 |
| 1000 |
| 786×4 |
| 1000 |


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
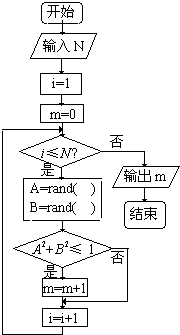 如图的程序框图可用来估计圆周率π的值.如果输入1200,输出的结果为943,则运用此方法,计算π的近似值为
如图的程序框图可用来估计圆周率π的值.如果输入1200,输出的结果为943,则运用此方法,计算π的近似值为查看答案和解析>>
科目:高中数学 来源: 题型:单选题
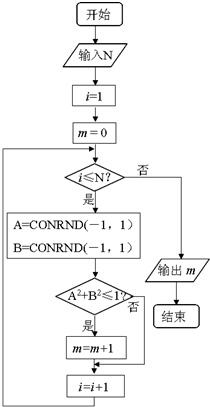 程序框图可用来估计圆周率π的值.设CONRND(-1,1)是产生随机数的函数,能随机产生区间(-1,1)内的任何一个数,如果输入1000,输出的结果为786,则运用此方法,计算π的近似值为
程序框图可用来估计圆周率π的值.设CONRND(-1,1)是产生随机数的函数,能随机产生区间(-1,1)内的任何一个数,如果输入1000,输出的结果为786,则运用此方法,计算π的近似值为查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省大连22中高二(下)4月月考数学试卷(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省巢湖市庐江中学高一综合检测数学试卷(必修3)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com