练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
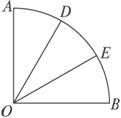
    如图3-3-4,在圆心角为90°的扇形中，以圆心O为起点作射线OC.求使得∠AOC和∠BOC都不小于30°的概率.

         图3-3-4

    解：A={作射线OC，使∠AOC和∠BOC都不小于30°}，作射线OD、OE，使∠AOD=30°，∠AOE=60°，当OC在∠DOE内时，使∠AOC和∠BOC都不小于30°，则P(A)=.

        巧解提示 其实，本题可以分别求扇形AOB、扇形DOE的面积，然后用几何概型的公式进行计算.但是，如果从角度的变化进行分析，显然弧DE的长度是弧AB的长度的，分析、计算更加简便.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

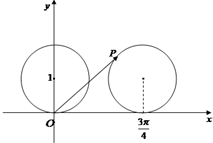    如图，在平面直角坐标系中，一单位圆的圆心的初始位置在（0，1），此时P点位置是原点，圆在x轴上沿正向滚动，当圆滚动到圆心位于（
    3π
    4
    ，1    ）时，
    OP
    的坐标为
    （
    3π
    4
    -
    		2
    2
    ，1+
    		2
    2
    ）
    （
    3π
    4
    -
    		2
    2
    ，1+
    		2
    2
    ）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

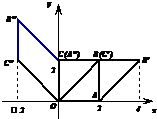    精英家教网（Ⅰ）如图，正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′，平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C''，求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵．
    （Ⅱ）在直角坐标系xOy中，圆O的参数方程为
    x=-
    		2
    2
    +rcosθ
    y=-
    		2
    2
    +rsinθ
    （θ为参数，r＞0）．以O为极点，x轴正半轴为极轴，并取相同的单位长度建立极坐标系，直线l的极坐标方程为ρsin(θ+
    π
    4
    )=
    		2
    2
    ．写出圆心的极标，并求当r为何值时，圆O上的点到直线l的最大距离为3．
    （Ⅲ）已知a2+2b2+3c2=6，若存在实数a，b，c，使得不等式a+2b+3c＞|x+1|成立，求实数x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

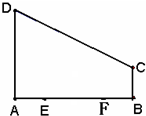    如图直角梯形ABCD中，∠DAB=90°，AD∥BC，E，F是AB边的四等分点，AB=4，BC=BF=AE=1，AD=3，P为在梯形区域内一动点，满足PE+PF=AB，记动点P的轨迹为Γ．
    （1）建立适当的平面直角坐标系，求轨迹Γ在该坐标系中的方程；
    （2）判断轨迹Γ与线段DC是否有交点，若有交点，求出交点位置；若没有交点，请说明理由；
    （3）证明D，E，F，C四点共圆，并求出该圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某校有一贫困学生因病需手术治疗，但现在还差手术费万元，团委计划在全校开展爱心募捐活动，为了增加活动的趣味性吸引更多学生参与，特举办“摇奖100%中奖”活动.凡捐款10元者，享受一次摇奖机会，如图是摇奖机的结构示意图，摇奖机的旋转盘是均匀的，扇形区域所对应的圆心角的比值分别为1：2：3：4：5.相应区域分别设立一、二、三、四、五等奖，奖品分别为价值分别为5元、4元、3元、2元、1元的学习用品.摇奖时，转动圆盘片刻，待停止后，固定指针指向哪个区域（边线忽略不计）即可获得相应价值的学习用品（如图指针指向区域，可获得价值3元的学习用品）.

    （Ⅰ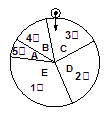）预计全校捐款10元者将会达到1500人次，那么除去

    购买学习用品的款项后，剩余款项是否能帮助该生完成手术治疗？

    （II）如果学生甲捐款20元，获得了两次摇奖机会，求他获得价

    值6元的学习用品的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图2-3-4,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB＝30°.

    求证:DC是⊙O的切线.

    图2-3-4

    查看答案和解析>>

    同步练习册答案