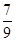��1���ɡ���a��b��c��R��ab��c=a��bc������ȡ���a��b��cΪ����������•c=a•��
��2��������{an} ��a1=0��an+1=2an+2����an=2n-2
��3����ƽ���ڡ������ε�����֮�ʹ��ڵ����ߡ�����ڿռ��С����������������������֮�ʹ��ڵ��ĸ���������
��4����M ��-2��0����N ��2��0��������MNΪб�ߵ�ֱ��������ֱ�Ƕ���P�Ĺ켣������x2+y2=4
�����ĸ������У��ó��Ľ�����ȷ���� ��д��������ȷ���۵���ţ�
���𰸡�
���������������ϳ˷�����ɣ�ͨ������������е�ͨ����������������������֮�ʹ��ڵ���������������x��ֵ1ʱ�����Եõ������ϵ��֮�ͣ����Dz�ͬ�ķ��Ų���ȷ��
����⣺�����������ϳ˷�����ɣ�
��
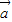
��
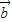
�ļн�ΪA��
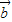
��
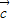
�ļн�ΪB����
��
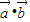
��
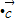
��ʾ��
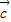
ƽ�е�������

•��
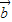
•
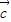
����ʾ��
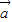
ƽ�е�������
��
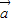
��
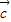
��һ��ƽ�У�
��
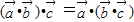
��һ��������
�ʣ�1������ȷ��
��a
n+1=2a
n+2��
��2+a
n+1=2��a
n+2����
��{a
n+2}��һ���ȱ����У�
��a
n=2
n-2���ʣ�2����ȷ��
������ƽ���ڡ������ε�����֮�ʹ��ڵ����ߡ�����ڿռ���
�����������������������֮�ʹ��ڵ�������������3����ȷ��
����x��ֵ1ʱ�����Եõ������ϵ��֮�ͣ����Dz�ͬ�ķ��Ų���ȷ���ʣ�4������ȷ��
�ʴ�Ϊ����2����3����
���������⿼��������������������������Ĺؼ�����ȷ������Ⱥ��ɵĺ��壬ע�Ȿ�����������ĸ����ⶼҪ��ȷ����������Ա��⣮

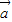 ��
��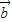 �ļн�ΪA��
�ļн�ΪA��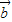 ��
��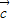 �ļн�ΪB����
�ļн�ΪB����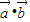 ��
��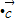 ��ʾ��
��ʾ��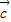 ƽ�е�������
ƽ�е������� •��
•��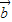 •
•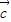 ����ʾ��
����ʾ��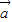 ƽ�е�������
ƽ�е�������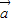 ��
��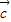 ��һ��ƽ�У�
��һ��ƽ�У�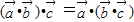 ��һ��������
��һ��������


 ��2011•�������ģ�����壺����Բ����������Ͷ����һ��������ɵ������γ�Ϊ����Բ�ġ����������Ρ������������Բ�ġ����������Ρ������Ƶģ������������Բ�ǡ�������Բ�������������ε����Ʊȳ�Ϊ��Բ�����Ʊȣ���֪��ԲC1��
��2011•�������ģ�����壺����Բ����������Ͷ����һ��������ɵ������γ�Ϊ����Բ�ġ����������Ρ������������Բ�ġ����������Ρ������Ƶģ������������Բ�ǡ�������Բ�������������ε����Ʊȳ�Ϊ��Բ�����Ʊȣ���֪��ԲC1�� B.
B.
 C.
C.
 D.
D.