
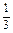 x3+
x3+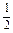 ax2+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时取得极小值,求点(a,b)对应的区域的面积以及
ax2+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时取得极小值,求点(a,b)对应的区域的面积以及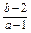 的取值范围.
的取值范围.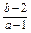
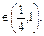
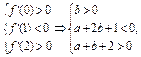
 如图阴影部分,其中点A(-3,1),B(-1,0),D(-2,0),
如图阴影部分,其中点A(-3,1),B(-1,0),D(-2,0),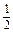 |BD|×h=
|BD|×h=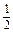 (h为点A到a轴的距离).
(h为点A到a轴的距离).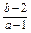 ,
,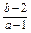
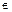 (kCA,kCB),
(kCA,kCB),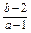
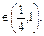


科目:高中数学 来源:不详 题型:解答题
 成本1 000元,运费500元,可得产品90kg,若采用乙种原料
成本1 000元,运费500元,可得产品90kg,若采用乙种原料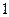 t成本1 500元,运费400元,可得产品100kg.若每日预算总成本不得超过6 000元,运费不得超过2 000元,此工厂每日最多可生产多少千克产品?
t成本1 500元,运费400元,可得产品100kg.若每日预算总成本不得超过6 000元,运费不得超过2 000元,此工厂每日最多可生产多少千克产品?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
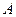 、
、 两种型号的帐篷中选择一种,
两种型号的帐篷中选择一种,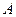 型号的帐篷比
型号的帐篷比 型号的少5顶.若只选
型号的少5顶.若只选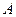 型号的,每顶帐篷住4人,则帐篷不够;每顶帐篷住5人,则有一顶帐篷没有住满.若只选
型号的,每顶帐篷住4人,则帐篷不够;每顶帐篷住5人,则有一顶帐篷没有住满.若只选 型号的,每顶帐篷住3人,则帐篷不够;每顶帐篷住4人,则有帐篷多余.设
型号的,每顶帐篷住3人,则帐篷不够;每顶帐篷住4人,则有帐篷多余.设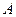 型号的帐篷有
型号的帐篷有 顶,用不等式将题目中的不等关系表示出来.
顶,用不等式将题目中的不等关系表示出来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com