
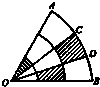
 如图,扇形AOB的圆心角为60°,半径为6cm,C,D分别是
如图,扇形AOB的圆心角为60°,半径为6cm,C,D分别是 | AB |
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
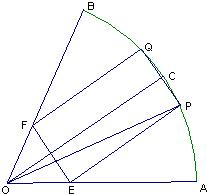 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
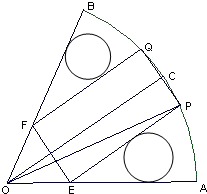 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
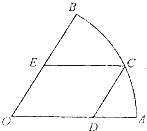 (2013•南京二模)如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在
(2013•南京二模)如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在 | AB |
查看答案和解析>>
科目:高中数学 来源:2002年全国各省市高考模拟试题汇编 题型:022
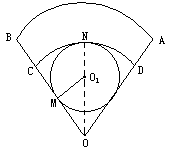
一扇形铁皮AOB,半径OA=72cm,圆心角∠AOB=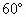 ,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图),则OC的长为________.
,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图),则OC的长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com