练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知：sin230°+sin290°+sin2150°= ；
    sin25°+sin265°+sin2125°= ；
    sin212°+sin272°+sin2132°= ；
    通过观察上述两等式的规律，请你写出一般性的命题，并给予的证明．

    【答案】解：一般形式：sin2α+sin2（α+60°）+sin2（α+120°）=
    证明 左边=
    =
    = ﹣sin2αsin240°]
    =
    = =右边
    ∴原式得证
    （将一般形式写成 sin2（α﹣60°）+sin2α+sin2（α+60°）= ，sin2（α﹣240°）+sin2（α﹣120°）+sin2α= 等均正确．）
    【解析】通过所给的等式归纳出一般形式，利用二倍角的余弦公式将等式的左边降幂求出左边的值，即得到证明．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=ln（1+x），g（x）=xf′（x），x≥0，其中f′（x）是f（x）的导函数．
    （1）g1（x）=g（x），gn+1（x）=g（gn（x）），n∈N+ ， 求g1（x），g2（x），g3（x），并猜想gn（x）的表达式（不必证明）；
    （2）若f（x）≥ag（x）恒成立，求实数a的取值范围；
    （3）设n∈N+ ， 比较g（1）+g（2）+…+g（n）与n﹣f（n）的大小，并用数学归纳法加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于的函数．

    （）当时，求函数在点处的切线方程．

    （）设，讨论函数的单调区间．

    （）若函数没有零点，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂有一批货物由海上从甲地运往乙地，已知轮船的最大航行速度为60海里/小时，甲地至乙地之间的海上航行距离为600海里，每小时的运输成本由燃料费和其它费用组成，轮船每小时的燃料费与轮船速度的平方成正比，比例系数为0．5，其它费用为每小时1250元．

    （1）请把全程运输成本（元）表示为速度（海里/小时）的函数,并指明定义域；

    （2）为使全程运输成本最小，轮船应以多大速度行驶？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三个数a、b、c∈（0， ），且cosa=a，sin（cosb）=b，cos（sinc）=c，则a、b、c从小到大的顺序是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量，，函数的最大值为.

    (1)求的大小；

    (2)将函数的图象向左平移个单位，再将所得图象上各点的横坐标缩短为原来的，纵坐标不变，得到函数的图象，作出函数在的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）若函数在处的切线平行于直线，求实数a的值；

    （Ⅱ）判断函数在区间上零点的个数；

    （Ⅲ）在（Ⅰ）的条件下，若在上存在一点，使得成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100]，若低于60分的人数是15人，则该班的学生人数是（ ）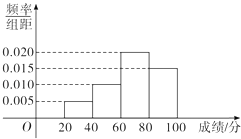

    A.45
    B.50
    C.55
    D.60

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两定点， ，曲线上的动点满足，直线与曲线的另一个交点为．

    （Ⅰ）求曲线的标准方程；

    （Ⅱ）设点，若，求直线的方程．

    查看答案和解析>>

    同步练习册答案