
分析 (1)求出y'=3x2+6ax+3b,由题意得12+12a+3b=0,且k=y′|x=1=3+6a+3b=-3,由此能求出a=-1,b=0,从而y=x3-3x2+c,则y'=3x2-6x,由此利用导数性质能求出函数的单调区间.
(2)由y'=3x2-6x=0,解得x=0,x=2,推导出函数在x=0时取得极大值c,在x=2时取得极小值c-4,从而能求出函数的极大值与极小值的差.
解答 解:(1)∵函数y=x3+3ax2+3bx+c,
∴y'=3x2+6ax+3b,
∵函数y=x3+3ax2+3bx+c在x=2处有极值,
∴当x=2时,y′=0,即12+12a+3b=0,①
∵函数图象在x=1处的切线与直线6x+2y+5=0平行,
∴k=y′|x=1=3+6a+3b=-3,②
联立①②,解得a=-1,b=0,
∴y=x3-3x2+c,则y'=3x2-6x,
令y'=3x2-6x>0,解得x<0或x>2,
令y'=3x2-6x<0,解得0<x<2,
∴函数的单调递增区间是(-∞,0),(2,+∞),单调递减区间是(0,2);
(2)由(1)可知,y'=3x2-6x,
令y′=0,即3x2-6x=0,解得x=0,x=2,
∵函数在(-∞,0)上单调递增,在(0,2)上单调递减,在(2,+∞)上单调递增,
∴函数在x=0时取得极大值c,在x=2时取得极小值c-4,
∴函数的极大值与极小值的差为c-(c-4)=4.
点评 本题考查函数的单调区间的求法,考查函数的极大值与极小值的差的求法,是中档题,解题时要认真审题,注意导数性质及导数的几何意义的合理运用.


科目:高中数学 来源: 题型:填空题
| 月收入2000元以下 | 月收入2000元及以上 | 总计 | |
| 高中文化以上 | 10 | 45 | 55 |
| 高中文化及以下 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若-2≤m<0,则函数f(x)=-x2+mx在区间(-4,-1)上单调递增 | |
| B. | “1≤x≤4”是“${log_{\frac{1}{5}}}$x≥-1”的充分不必要条件 | |
| C. | x=$\frac{π}{3}$是函数f(x)=cos 2x-$\sqrt{3}$sin 2x的一条对称轴 | |
| D. | 若a∈[$\frac{1}{2}$,6),则函数f(x)=$\frac{1}{2}$x2-alnx在区间(1,3)上有极值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分且必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
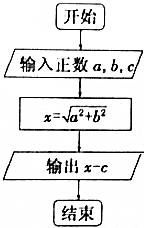 已知在平面直角坐标系中有一个圆心在坐标原点,半径为c的圆,(a,b)为任一点.则如图所示的程序框图表示的算法的作用是判断点(a,b)与圆心在坐标原点,半径为c的圆的位置关系.
已知在平面直角坐标系中有一个圆心在坐标原点,半径为c的圆,(a,b)为任一点.则如图所示的程序框图表示的算法的作用是判断点(a,b)与圆心在坐标原点,半径为c的圆的位置关系.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln(a-b)>0 | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | 3a-b<1 | D. | loga2<logb2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com