
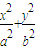 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.
,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.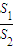 =
= ?请说明理由.
?请说明理由.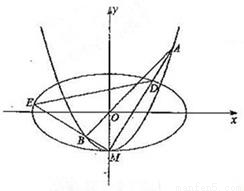
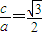 ,从而a=2b,又2
,从而a=2b,又2 =a,解得a=2,b=1,
=a,解得a=2,b=1, ,y=x2-1.
,y=x2-1.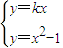 得x2-kx-1=0.
得x2-kx-1=0.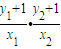 =
=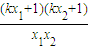 =
=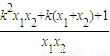 =
=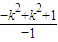 =-1.
=-1.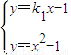 ,解得
,解得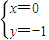 或
或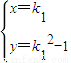 .
.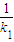 ,同理可得点B的坐标为(-
,同理可得点B的坐标为(-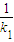 ,
,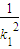 -1).
-1). |MA|•|MB|=
|MA|•|MB|=
 •|k1|•
•|k1|•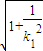 •|-
•|-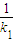 |=
|= .
. 得(1+4k12)x2-8k1x=0.
得(1+4k12)x2-8k1x=0.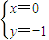 或,
或,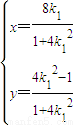 ,则点D的坐标为(
,则点D的坐标为(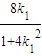 ,
, ).
).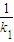 .同理可得点E的坐标为(
.同理可得点E的坐标为(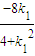 ,
, ).
). |MD|•|ME|=
|MD|•|ME|=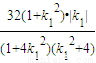 .
.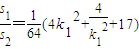 =
= ,解得k12=4或k12=
,解得k12=4或k12= .
.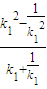 =k1-
=k1-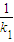 .所以k=±
.所以k=± .
. x和y=-
x和y=- x.
x.

 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
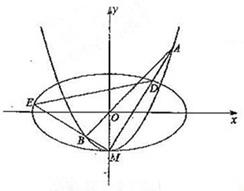 如图,椭圆C1:
如图,椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| S1 |
| S2 |
| 17 |
| 32 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省宜昌市宜都一中高二(下)3月月考数学试卷(理科)(解析版) 题型:解答题
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.
,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长. =
=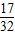 ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省杭州市西湖区学军中学高二(上)期末数学试卷(理科)(解析版) 题型:解答题
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.
,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.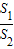 =
= ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013年高考数学压轴大题训练:圆锥曲线的方程与性质(解析版) 题型:解答题
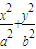 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为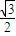 ,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.
,x轴被曲线C2:y=x2-b截得的线段长等于C1的长半轴长.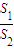 =
=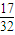 ?请说明理由.
?请说明理由.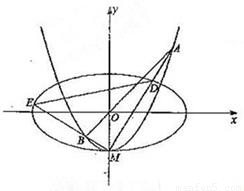
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com