练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，平面四边形中，,,,，将三角形沿翻折到三角形的位置，平面平面，为中点.

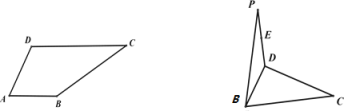
    （Ⅰ）求证：；

    （Ⅱ）求直线与平面所成角的正弦值.

    【答案】(Ⅰ)详见解析(Ⅱ)

    【解析】

    （Ⅰ）由题意为等边三角形，可以证明及，由平面平面，可知平面，从而，进而可以得到平面，即可证明；(Ⅱ)以为坐标原点，分别为轴，轴建立空间直角坐标系，分别求出和平面的法向量，由可以得到答案。

    （Ⅰ）由题意为等边三角形，则，

    在三角形中，,，由余弦定理可求得，

    ，即

    又平面平面，平面平面，平面

    平面

    等边三角形中，为中点，则，且

    平面，

    （Ⅱ）以为坐标原点，分别为轴，轴建立空间直角坐标系，

    则，，，，

    ，

    设是平面的法向量，则，

    取

    所以直线与平面所成角的正弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在创建“全国文明卫生城”过程中，某市“创城办”为了调查市民对创城工作的了解情况，进行了一次创城知识问卷调查（一位市民只能参加一次）．通过随机抽样，得到参加问卷调查的100人的得分统计结果如表所示：

    组别

    [30，40）

    [40，50）

    [50，60）

    [60，70）

    [70，80）

    [80，90）

    [90，100]

    频数

    2

    15

    20

    25

    24

    10

    4

    （I）由频数分布表可以大致认为，此次问卷调查的得分Z服从正态分布N（μ，198），μ近似为这100人得分的平均值（同一组中的数据用该组区间的中点值作代表），利用该正态分布，求P（37＜Z≤79）；

    （II）在（I）的条件下，“创城办”为此次参加问卷调查的市民制定如下奖励方案：

    ①得分不低于μ的可以获赠2次随机话费，得分低于μ的可以获赠1次随机话费；

    ②每次获赠的随机话费和对应的概率为：

    赠送话费的金额（单元：元）

    20

    40

    概率

    现有市民甲参加此次问卷调查，记ξ（单位：元）为该市民参加问卷调查获赠的话费，求ξ的分布列与数学期望．附：参考数据与公式：14．

    若X～N（μ，σ2），则P（μ﹣σ＜X≤μ+σ）＝0.6826；P（μ2σ＜X≤μ+2σ）＝0.9544，P（μ﹣3σ＜X≤μ+3σ）＝0.9974．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某水果批发商销售进价为每箱40元的苹果，假设每箱售价不低于50元且不得高于55元，市场调查发现，若每箱以50元的价格销售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱.

    （1）求平均每天的销售量y（箱）与销售单价x（元/箱）之间的函数关系式.

    （2）求该批发商平均每天的销售利润w（元）与销售单价x（元/箱）之间的函数关系式.

    （3）当每箱苹果的售价为多少元时，每天可以获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为直角梯形， ， ， ， 与均为等边三角形，点为的中点.

    （1）证明：平面平面；

    （2）若点在线段上且，求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC在内角A、B、C的对边分别为a，b，c，已知a=bcosC+csinB.

    （Ⅰ）求B；

    （Ⅱ）若b=2，求△ABC面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）设是的极值点，求的值；

    （Ⅱ）在（Ⅰ）的条件下，在定义域内恒成立，求的取值范围；

    （Ⅲ）当时，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图①，在等腰梯形中，，，分别为，的中点，，为中点现将四边形沿折起,使平面平面，得到如图②所示的多面体在图②中，

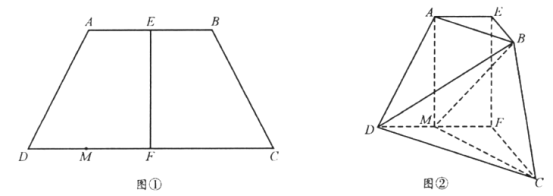
    （1）证明：；

    （2）求二面角的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，曲线的参数方程为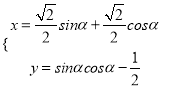（为参数），若以直角坐标系中的原点为极点， 轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为（为实数.）

    （1）求曲线的普通方程和曲线的直角坐标方程；

    （2）若曲线与曲线有公共点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的中心在原点，直线与坐标轴的交点是椭圆的两个顶点.

    （1）求椭圆的方程；

    （2）若是椭圆上的两点，且满足，求的最小值.

    查看答案和解析>>

    同步练习册答案