
【题目】已知x∈(1,+∞),函数f(x)=ex+2ax(a∈R),函数g(x)=| ![]() ﹣lnx|+lnx,其中e为自然对数的底数.
﹣lnx|+lnx,其中e为自然对数的底数.
(1)若a=﹣ ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)证明:当a∈(2,+∞)时,f′(x﹣1)>g(x)+a.
【答案】
(1)解:当a=﹣ ![]() ,f(x)=ex﹣e2x,x∈(1,+∞),
,f(x)=ex﹣e2x,x∈(1,+∞),
f′(x)=ex﹣e2,
当x∈(1,2)时,f′(x)<0,f(x)在(1,2)上单调递减;
当x∈(1,+∞)时,f′(x)>0,f(x)在(2,+∞)上单调递增
(2)证明: x∈(1,+∞),f′(x﹣1)=ex﹣1+2a,
g(x)=| ![]() ﹣lnx|+lnx=
﹣lnx|+lnx=  ,
,
①1<x<e时,证明当a∈(2,+∞)时,f′(x﹣1)>g(x)+a,
即证明:ex﹣1+2a> ![]() +a,a>2,
+a,a>2,
即a> ![]() ﹣ex﹣1,
﹣ex﹣1,
只需证明h(x)= ![]() ﹣ex﹣1≤2在(1,e)恒成立即可,
﹣ex﹣1≤2在(1,e)恒成立即可,
h′(x)=﹣ ![]() ﹣ex﹣1<0,h(x)在(1,e)递减,
﹣ex﹣1<0,h(x)在(1,e)递减,
h(x)最大值=h(1)=e﹣1<2,
∴a> ![]() ﹣ex﹣1,
﹣ex﹣1,
∴1<x<e时,当a∈(2,+∞)时,f′(x﹣1)>g(x)+a;
②x≥e时,证明当a∈(2,+∞)时,f′(x﹣1)>g(x)+a,
即证明:ex﹣1+2a>2lnx﹣ ![]() +a,a>2,
+a,a>2,
令m(x)=ex﹣1﹣2lnx+ ![]() +a,(a>0,x≥e),
+a,(a>0,x≥e),
m′(x)=﹣ ![]() ﹣
﹣ ![]() +ex﹣1,显然m′(x)在[e,+∞)递增,
+ex﹣1,显然m′(x)在[e,+∞)递增,
而m′(e)= ![]() ≈0,m′(3)≈6,
≈0,m′(3)≈6,
近似看成m(x)在[e,+∞)递增,
∴m(x)>m(x0)≈m(e)=ee﹣1+a﹣1>ee﹣1+1>0,
综上,当a∈(2,+∞)时,f′(x﹣1)>g(x)+a
【解析】(1)把a=﹣ ![]() 代入函数解析式,求出函数的导函数由导函数的符号求得函数的单调区间;(2)求出f′(x﹣1)的表达式以及g(x)的分段函数,通过讨论1<x<e和 x≥e的范围分别证明得答案.
代入函数解析式,求出函数的导函数由导函数的符号求得函数的单调区间;(2)求出f′(x﹣1)的表达式以及g(x)的分段函数,通过讨论1<x<e和 x≥e的范围分别证明得答案.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的最大(小)值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.
比较,其中最大的是一个最大值,最小的是最小值即可以解答此题.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】正项等比数列{an},若2a1+3a2=1,a32=9a2a6 .
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+log3a3+…log3an , 求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆x2+y2﹣12x+32=0的圆心为Q,过点P(0,2)且斜率为k的直线与圆Q相交于不同的两点A,B.
(1)求k的取值范围;
(2)是否存在常数k,使得向量 ![]() 与
与 ![]() 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
(1)求与圆C相切,且与直线l垂直的直线方程;
(2)在直线OA上(O为坐标原点),存在定点B(不同于点A),满足:对于圆C上任一点P,都有![]() 为一常数,试求所有满足条件的点B的坐标.
为一常数,试求所有满足条件的点B的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
如图,⊙O在平面![]() 内,AB是⊙O的直径,
内,AB是⊙O的直径,![]() 平面
平面![]() ,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求证:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (x>0),观察:
(x>0),观察:
f1(x)=f(x)= ![]() ,
,
f2(x)=f(f1(x))= ![]() ;
;
f3(x)=f(f2(x))= ![]() .
.
f4(x)=f(f3(x))= ![]()
…
根据以上事实,当n∈N*时,由归纳推理可得:fn(1)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如图频率分布直方图:
附:临界值参考公式: ![]() ,n=a+b+c+d.
,n=a+b+c+d.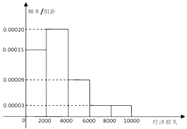
(1)试根据频率分布直方图估计小区平均每户居民的平均损失(同一组中的数据用该组区间的中点值作代表);
(2)小明向班级同学发出倡议,为该小区居民损款,现从损失超过4000元的居民中随机抽出2户进行捐款援助,投抽出损失超过8000元的居民为ξ户,求ξ的分布列和数学期望;
(3)台风后区委会号召该小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如表,在表格空白外填写正确数字,并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 | 30 | ||
损款不超过500元 | 6 | ||
合计 |
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知点A(-1,-2),B(1,3),P为x轴上的一点,求|PA|+|PB|的最小值;
(2)已知点A(2,2),B(3,4),P为x轴上一点,求||PB|-|PA||的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为 ![]() (θ为参数).以原点O为极点,x轴的非负半轴为极轴建立极坐标方程.
(θ为参数).以原点O为极点,x轴的非负半轴为极轴建立极坐标方程.
(1)求曲线C的极坐标方程;
(2)若直线l:θ=α(α∈[0,π),ρ∈R)与曲线C相交于A,B两点,设线段AB的中点为M,求|OM|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com