
 、乙答对的概率是
、乙答对的概率是 .(1)分别求甲、乙两人能通过一试进入二试的概率
.(1)分别求甲、乙两人能通过一试进入二试的概率 、
、 ;(2)求甲、乙两人都能被录用的概率
;(2)求甲、乙两人都能被录用的概率 .
.科目:高中数学 来源:不详 题型:解答题
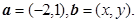
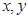 分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足
分别表示将一枚质地均匀的骰子先后抛掷两次时第一次、第二次正面朝上出现的点数,求满足 的概率.
的概率.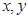 在连续区间[1,6]上取值,求满足
在连续区间[1,6]上取值,求满足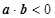 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
 件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过
件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过 克的概率.
克的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
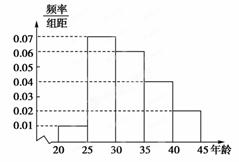
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
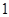 ,
,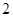 ,
,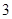 ,
,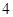 ,
,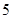 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下: | 等级 | 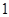 | 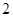 | 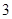 | 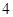 | 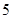 |
| 频率 | 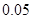 | 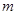 | 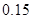 | 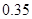 | 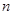 |
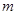 ,
,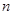 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com