
已知函数 (
( ,c是实数常数)的图像上的一个最高点
,c是实数常数)的图像上的一个最高点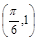 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是 ,
,
(1)求函数 的解析式及其单调增区间;
的解析式及其单调增区间;
(2)在△ABC中,角A、B、C所对的边分别为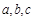 ,且
,且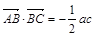 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当 时,试求函数
时,试求函数 的取值范围.
的取值范围.
(1) ,单调递增区间是
,单调递增区间是 ;(2)
;(2) .
.
【解析】
试题分析:(1)三角函数问题一般都要化为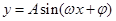
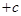 的一个三角函数的形式,然后才可利用正弦函数的性质解题,这个函数图象上相邻有最高点与最低点的横坐标之差的绝对值为半个周期,而周期
的一个三角函数的形式,然后才可利用正弦函数的性质解题,这个函数图象上相邻有最高点与最低点的横坐标之差的绝对值为半个周期,而周期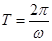 ,再加上最高(低)点在函数图象上,我们就可出这个函数的解析式了(
,再加上最高(低)点在函数图象上,我们就可出这个函数的解析式了(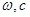 );(2)由
);(2)由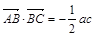 ,根据向量数量积定义我们可求出
,根据向量数量积定义我们可求出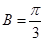 ,那么三角形的另一内角
,那么三角形的另一内角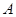 的范围应该是
的范围应该是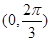 ,即函数
,即函数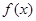 中
中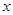 的范围是
的范围是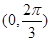 ,然后我们把
,然后我们把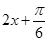 一个整体,得出
一个整体,得出 ,而正弦函数
,而正弦函数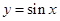 在
在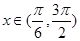 时取值范围是
时取值范围是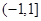 ,因此可求出
,因此可求出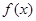 的值域.
的值域.
试题解析:(1)∵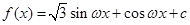 ,
,
∴ .
.
∵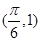 和
和 分别是函数图像上相邻的最高点和最低点,
分别是函数图像上相邻的最高点和最低点,
∴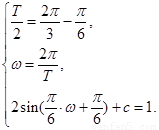 解得
解得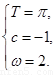
∴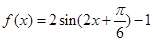 .
.
由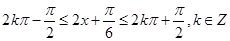 ,解得
,解得 .
.
∴函数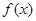 的单调递增区间是
的单调递增区间是 .
.
(2)∵在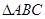 中,
中,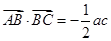 ,
,
∴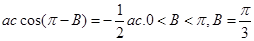 .
.
∴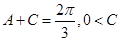 ,即
,即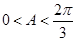 .
.
∴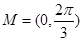 .
.
当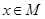 时,
时, ,考察正弦函数
,考察正弦函数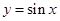 的图像,可知,
的图像,可知,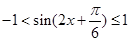 .
.
∴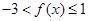 ,即函数
,即函数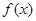 的取值范围是
的取值范围是 .
.
考点:(1)五点法与函数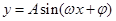
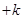 的图象;(2)三角函数在给定区间的值域.
的图象;(2)三角函数在给定区间的值域.


科目:高中数学 来源:2006-2007年福建泉州一中、五中、七中高三联考数学试题 题型:044
(文)已知函数![]() ,其中C是实数,
,其中C是实数,
(Ⅰ)求f(x)的极大值和极小值;
(Ⅱ)证明方程f(x)=0的不同实根的个数不大于3.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年上海黄浦区高三上学期期末考试(即一模)理数学卷(解析版) 题型:解答题
已知函数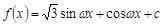 (
(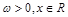 ,c是实数常数)的图像上的一个最高点
,c是实数常数)的图像上的一个最高点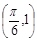 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是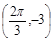 ,
,
(1)求函数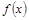 的解析式及其单调增区间;
的解析式及其单调增区间;
(2)在△ABC中,角A、B、C所对的边分别为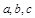 ,且
,且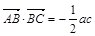 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当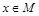 时,试求函数
时,试求函数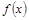 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年吉林通化第一中学高三上学期第二次月考理科数学试卷(解析版) 题型:选择题
已知函数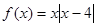
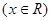 ,若存在正实数
,若存在正实数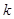 ,使得方程
,使得方程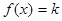 有两个根
有两个根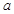 ,
,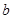 ,其中
,其中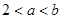 ,则
,则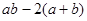 的取值范围是( )
的取值范围是( )
A.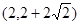 B.
B.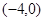 C.
C.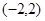 D.
D.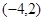
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com